Working with matrices in Python#

Matrices can be described by multidimensional numpy arrays, and we can perform matrix multiplication with the numpy.matmul() function. [1]

import numpy as np

r = np.array([3,4])
M = np.array([[0,-1],
              [1, 0]])
r_prime = np.matmul(M, r)
print(r_prime)

[-4  3]

The inverse of a matrix can be calculated (if it exists) using numpy.linalg.inv().

N = np.linalg.inv(M)
print(N)

[[ 0.  1.]
 [-1. -0.]]

np.matmul(N, r_prime) # we should recover our original vector

array([3., 4.])

Matrix–matrix multiplication can also be performed using numpy.matmul():

MM = np.matmul(M,M) # Two 90 degree rotations should be a 180 degree rotation.
print(MM)

[[-1  0]
 [ 0 -1]]

Exercise#

Download the following files and add them to the working directory of your JupyterHub: visualisation.py and water.txt. The first file is a text file containing a single Python function (we will explain how to package functions into your own modules later in the course). The second file contains the atomistic coordinates for a water molecule. Let us read in the water molecule coordinates, and use the visualisation.show() function to have a look.

import visualisation
x, y, z = np.loadtxt('water.txt', unpack=True)
visualisation.show(x, y)
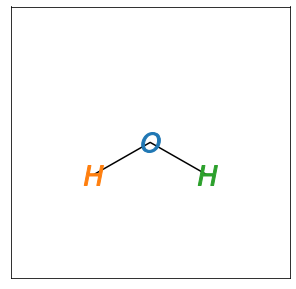
../_images/fd07006e120cdd413a046ce02f86ce2c621cca007536380a4bc7c91f83cc10a1.png

You will notice that we do not pass the z-coordinates to the visualisation script. This is because:

  1. 3D visualisation is a bit tricky and we want to focus on the understanding of the matrix operations.

  2. We are only going to focus on the rotation in the xy-plane (so the z-coordinate will never change).

The exercise this week is to use matrices and vector to rotate this molecule in the xy-plane. First, you should write a function that will return a NumPy matrix when passed some angle, \(\beta\), with the form,

\[\begin{split} \begin{bmatrix}\cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{bmatrix} \end{split}\]

This is called a rotation matrix, a rotation matrix in a linear algebra tool that lets us rotate something in Euclidean space such as the cartesian coordinate system that we use to describe the atomic positions. Remember that the NumPy cos and sin functions will expect the angle to be in radians!

Then use the rotation matrix to obtain new coordinates for the water molecule, by performing the following matrix multiplication.

\[\begin{split} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix}\cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{bmatrix} \begin{bmatrix}x \\ y \end{bmatrix} \end{split}\]

where \(x\) and \(y\) are the current positions of the x- and y-coordinates respectively and \(x'\) and \(y'\) are the rotated coordinates. Use the visualisation.show() function to help check that the rotation has been successful.