Newton’s method

A potentially more efficient method for minimisation is the potential energy function is Newton’s method (developed by Isaac Newton). This method uses both the first and second derivatives of the potential energy, the latter is found from the following equation,

\[ E''(r_{ij}) = 156\frac{A}{r_{ij}^{14}} - 42\frac{B}{r_{ij}^8}, \]

where again, the parameters are given previously.

The second derivative of a function describes the curvature of the function and can offer a more direct root to the minimum energy solution. The algorithm for Newton’s method is identical to the gradient descent method, but the update formula is changed to,

\[ r_{\text{new}} = r_{\text{old}} - \frac{E'(r_{ij})}{E''(r_{ij})},\]

where the parameters are introduced previously. As can be seen, this method has the benefit that there is no need to determine a hyperparameter. Additionally, under certain circumstances, it can be more efficient than the gradient descent method.

Newton’s method in action is shown below.

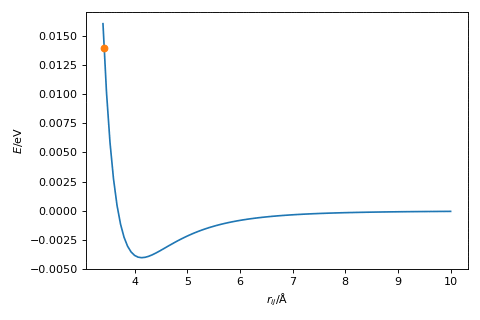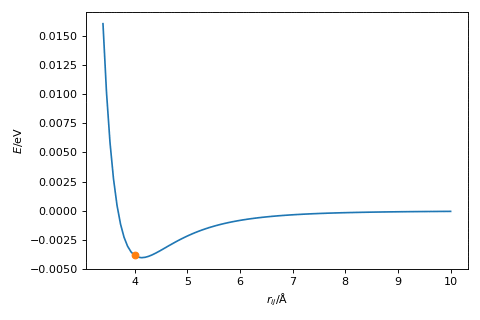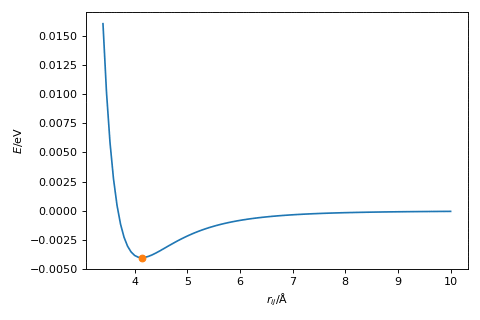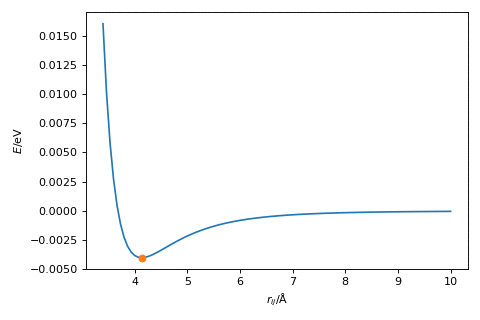
Exercise:

Implement Newton’s method algorithm for the same system as previously. Investigate how the algorithm performs against the gradient descent method for starting points of \(3.2\) Å, \(4.4\) Å, and \(6.0\) Å (consider the cause of the result for Newton’s method starting at \(6.0\) Å).