Radial distribution function
The scattering from a particle may be thought of as a Fourier transform of the radial distribution function (RDF) in the simulation. The RDF is the probability that a particle will be found at a given distance from another. We are able to visualise the RDF from a pylj simulation using the following code (at the end of the simulation, the average RDF will be presented).
from pylj import md, sample
def md_simulation(number_of_particles, temperature,
box_length, number_of_steps,
sample_frequency):
"""
Runs a molecular dynamics simulation in using the pylj
molecular dynamics engine.
Parameters
----------
number_of_particles: int
The number of particles in the simulation
temperature: float
The temperature for the initialisation and
thermostating
box_length: float
The length of the simulation square
number_of_steps: int
The number of molecular dynamics steps to run
sample_frequency:
How regularly the visualisation should be updated
Returns
-------
pylj.util.System
The complete system information from pylj
"""
%matplotlib notebook
system = md.initialise(number_of_particles, temperature,
box_length, 'square')
sample_system = sample.RDF(system)
system.time = 0
for i in range(0, number_of_steps):
system.integrate(md.velocity_verlet)
system.md_sample()
system.heat_bath(temperature)
system.time += system.timestep_length
system.step += 1
if system.step % sample_frequency == 0:
sample_system.update(system)
sample_system.average()
return system
system = md_simulation(20, 300, 20, 2000, 25)
If we vary the temperature or particle density of the simulation we should see changed in the RDF. Compare the RDFs you obtain to those shown below and consider which of a, b, and c represent a solid, liquid and a gas.
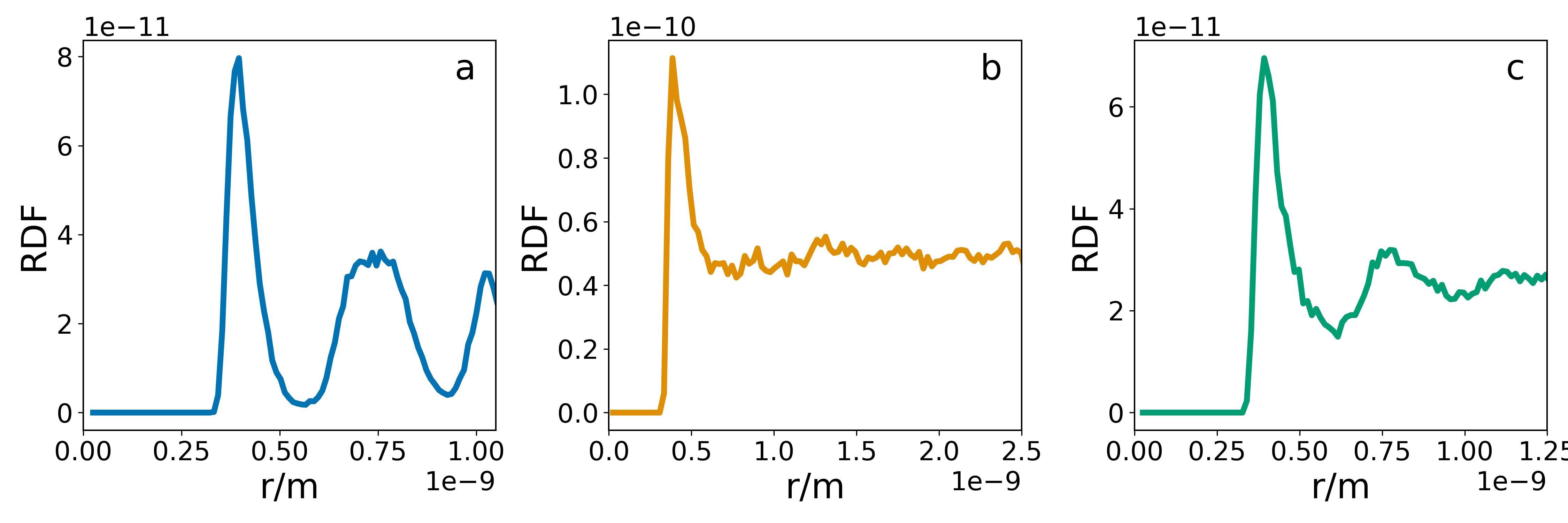
Figure 1. Radial distribution functions at different experimental conditions.