Build an MD simulation
We can now build our own one-dimensional molecular dynamics simulation. The Python code contains everything we need to build the MD simulation. Read though it (much of it has been discussed previously) and try to understand the flow of the code before running it to see what happens.
import numpy as np
import matplotlib.pyplot as plt
from scipy.constants import Boltzmann
mass_of_argon = 39.948 # amu
def lj_force(r, epsilon, sigma):
"""
Implementation of the Lennard-Jones potential
to calculate the force of the interaction.
Parameters
----------
r: float
Distance between two particles (Å)
epsilon: float
Potential energy at the equilibrium bond
length (eV)
sigma: float
Distance at which the potential energy is
zero (Å)
Returns
-------
float
Force of the van der Waals interaction (eV/Å)
"""
return 48 * epsilon * np.power(
sigma, 12) / np.power(
r, 13) - 24 * epsilon * np.power(
sigma, 6) / np.power(r, 7)
def init_velocity(T, number_of_particles):
"""
Initialise the velocities for a series of
particles.
Parameters
----------
T: float
Temperature of the system at
initialisation (K)
number_of_particles: int
Number of particles in the system
Returns
-------
ndarray of floats
Initial velocities for a series of
particles (eVs/Åamu)
"""
R = np.random.rand(number_of_particles) - 0.5
return R * np.sqrt(Boltzmann * T / (
mass_of_argon * 1.602e-19))
def get_accelerations(positions):
"""
Calculate the acceleration on each particle
as a result of each other particle.
N.B. We use the Python convention of
numbering from 0.
Parameters
----------
positions: ndarray of floats
The positions, in a single dimension,
for all of the particles
Returns
-------
ndarray of floats
The acceleration on each
particle (eV/Åamu)
"""
accel_x = np.zeros((positions.size, positions.size))
for i in range(0, positions.size - 1):
for j in range(i + 1, positions.size):
r_x = positions[j] - positions[i]
rmag = np.sqrt(r_x * r_x)
force_scalar = lj_force(rmag, 0.0103, 3.4)
force_x = force_scalar * r_x / rmag
accel_x[i, j] = force_x / mass_of_argon
accel_x[j, i] = - force_x / mass_of_argon
return np.sum(accel_x, axis=0)
def update_pos(x, v, a, dt):
"""
Update the particle positions.
Parameters
----------
x: ndarray of floats
The positions of the particles in a
single dimension
v: ndarray of floats
The velocities of the particles in a
single dimension
a: ndarray of floats
The accelerations of the particles in a
single dimension
dt: float
The timestep length
Returns
-------
ndarray of floats:
New positions of the particles in a single
dimension
"""
return x + v * dt + 0.5 * a * dt * dt
def update_velo(v, a, a1, dt):
"""
Update the particle velocities.
Parameters
----------
v: ndarray of floats
The velocities of the particles in a
single dimension (eVs/Åamu)
a: ndarray of floats
The accelerations of the particles in a
single dimension at the previous
timestep (eV/Åamu)
a1: ndarray of floats
The accelerations of the particles in a
single dimension at the current
timestep (eV/Åamu)
dt: float
The timestep length
Returns
-------
ndarray of floats:
New velocities of the particles in a
single dimension (eVs/Åamu)
"""
return v + 0.5 * (a + a1) * dt
def run_md(dt, number_of_steps, initial_temp, x):
"""
Run a MD simulation.
Parameters
----------
dt: float
The timestep length (s)
number_of_steps: int
Number of iterations in the simulation
initial_temp: float
Temperature of the system at
initialisation (K)
x: ndarray of floats
The initial positions of the particles in a
single dimension (Å)
Returns
-------
ndarray of floats
The positions for all of the particles
throughout the simulation (Å)
"""
positions = np.zeros((number_of_steps, 3))
v = init_velocity(initial_temp, 3)
a = get_accelerations(x)
for i in range(number_of_steps):
x = update_pos(x, v, a, dt)
a1 = get_accelerations(x)
v = update_velo(v, a, a1, dt)
a = np.array(a1)
positions[i, :] = x
return positions
x = np.array([1, 5, 10])
sim_pos = run_md(0.1, 10000, 300, x)
%matplotlib inline
for i in range(sim_pos.shape[1]):
plt.plot(sim_pos[:, i], '.', label='atom {}'.format(i))
plt.xlabel(r'Step')
plt.ylabel(r'$x$-Position/Å')
plt.legend(frameon=False)
plt.show()
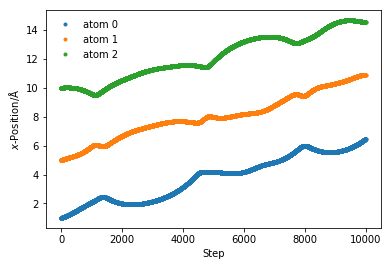
We can see how the particles interact with each other separated by about the minimum of the LJ and moving in tandem through the system.
It is possible to run the simulation at a series of different initial starting positions by varying values in the array x.