In the previous tutorial, flow controls were introduced which allow the manipulation/determination of data based on certain characteristics. This took the form If A is true then complete action B. Often there are more than one criteria that one wished to evaluate against, for example in the cases of If A and B are true then complete action C or If A or B are true then complete action C. Alternatively we coult want a criteria such as If A is False then complete action B.
Python can enact all these processes using and, or, and not statements. These statements collectively are called Boolean logic statements, named after the mathematician George Boole who created this field of mathematics. These statements are the building blocks of computers and Boolean logic is fundamentally important in all computation.
In this tutorial these logic statements will be used in combination with flow controls to manipulate some data from the first twenty elements of the periodic table. In order to get started, we shall first import the data that we require and explain how the data is stored.
from periodic_table_20 import periodic_table_20
The periodic_table_20 variable is a dictionary that contains dictionaries of properties of the the elements. The keys of the main dictionary are the chemical symbols of the first twenty elements. For example, to observe information about hydrogen we use
periodic_table_20["H"]
The information stored about each element is its: relative atomic mass, group, period, block, melting point, and boiling point. The keys of the elemental dictionary are mass, group, period, block, melting_point, and boiling_point. In order to obtain the block that hydrogen is in we can use
periodic_table_20["H"]["block"]
This indicates that, as we know, hydrogen lies in the s block of the periodic table.
If a periodic table is not to hand it may be difficult to remember the group and period of an element. However, Boolean statements can be used to determine the location of an element if a guess is given. To check whether phosphorus is in period 2 and group 15, the following python code can be used
if periodic_table_20["P"]["period"] == 2 and periodic_table_20["P"]["group"] == 15:
print("Correct, phosphorus is in period 2 and group 15!")
else:
print("Phosphorus is not in period 2 and group 15")
This is incorrect, as one would expect. Phosphorus is in period 3. Whilst phosphorus is in group 15, it is not in period 2 so the code "flows to" the else statement. What if we use the following code?
if periodic_table_20["P"]["period"] == 3 and periodic_table_20["P"]["group"] == 15:
print("Correct, phosphorus is in period 3 and group 15!")
else:
print("Phosphorus is not in period 3 and group 15")
Now we have provided the correct information for phosphorus the code is correct. But what will happen if we replace the and statement for an or statement? We will keep the incorrect guess of period 2 though.
if periodic_table_20["P"]["period"] == 2 or periodic_table_20["P"]["group"] == 15:
print("Correct, phosphorus is in period 2 or group 15!")
else:
print("Phosphorus is not in period 2 or group 15")
This states that we are correct as whilst phosphorus is not in period 2, it is in group 15. Therefore one of the two statements is true, and so the code "flow through" the if statement instead of the else statement. To better understand the process of what python is doing, the concept of truth tables is introduced. Below is a truth table for the and and or statements.
| A | B | AND | OR |
|---|---|---|---|
| True | True | True | True |
| True | False | False | True |
| False | True | False | True |
| False | False | False | False |
The truth tables give the output of the and and or statements when two statements, A and B, are evaluated. For example, taking the first line, if both statement A and statement B are true then A and B and A or B will both give true.
The outputs shown in the above diagrams are the same as those in the logic table. We can use the logic illustrated above to show what is happening in the examples above. Step by step the first example's logic follows:
1) periodic_table_20["P"]["period"] == 2, is evaluated which is False as phosphorus is in period 3.
2) periodic_table_20["P"]["group"] == 15 is evaluated which is True as phosphorus is in group 15.
3) False and True is evaluated which overall gives False.
4) if False is evaluated and the line "Phosphorus is not in period 2 and group 15" is printed through the else statement.
While in the third example the following logic occurs:
1) periodic_table_20["P"]["period"] == 2, is evaluated which is False as phosphorus is in period 3.
2) periodic_table_20["P"]["group"] == 15 is evaluated which is True as phosphorus is in group 15.
3) False or True is evaluated which overall gives True.
4) if True is evaluated and the line "Correct, phosphorus is in period 2 or group 15!" is printed.
Other statements can be evaluated. For example, if we wanted to determine whether lithium is liquid at 700 K we could use the following code
if periodic_table_20["Li"]["melting_point"] < 700 and periodic_table_20["Li"]["boiling_point"] > 700:
print("Lithium is liquid at 700 K")
else:
print("Lithium is not liquid at 700 K.")
This indicatrs that the melting point of lithium is below 700 K and its boiling point is greater than 700 K. Therefore lithium is liquid at 700 K.
Exercise: Write a similar code to determine whether sodium is a liquid at 100 $^{\circ}$C. Remember the melting and boiling points are recorded in K.
### Write your code here
Chemical molecules can also behave as logic gates. For example the molecule below was determined to be useful in detecting cancers by Ozlam and Akkaya$^{1}$. The molecule facilitates the transfer of singlet oxygen to triplet oxygen in the presence of both high concentrations of sodium ions and protons when irradiated with 660 nm radiation.
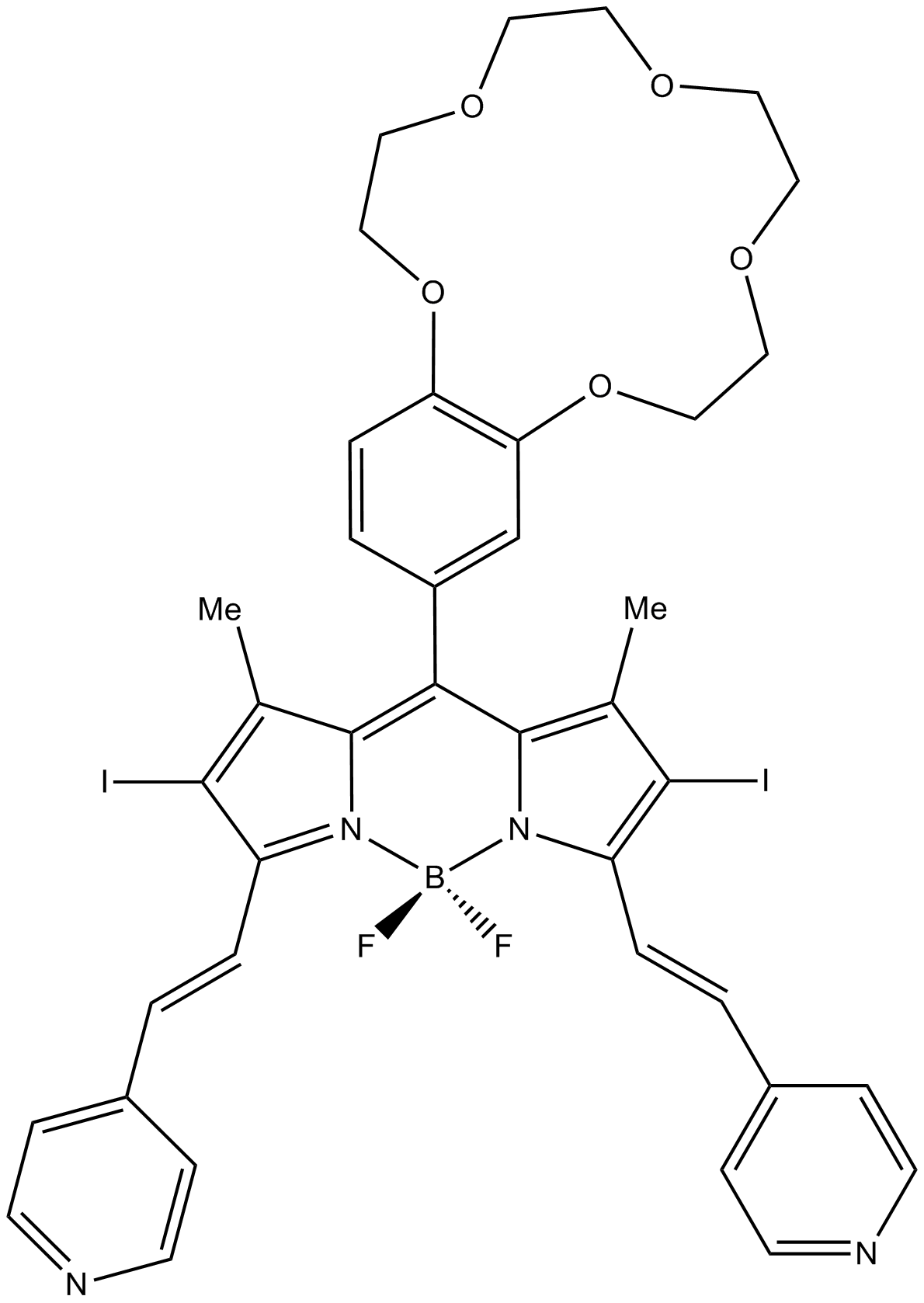
The concentration of sodium ions and protons are high in the presence of cancers. The transfer of singlet oxygen to triplet oxygen does not occur with the aid of this molecule unless both sodium ions and proton concentrations are high. This makes the "truth table" as follows:
| Sodium ion concentration | Proton concentration | Oxygen state |
|---|---|---|
| High | High | Triplet |
| High | Low | Singlet |
| Low | High | Singlet |
| Low | Low | Singlet |
This is analagous to the AND truth table as the production of triplet oxygen requires a high concentration of oxygen and a high concentration of sodium. Therefore the molecule above can aid in the detection of cancers using Boolean logic. There are other molecules that behave as logic gates for a multitude of other uses.
$^{1}$ S. Ozlam and E. U. Akkaya, J. Am. Chem. Soc. 2009, 131, 1, 48-49.
Not statements
The third aspect of Boolean logic is the not statement. The not statement simply reverses a Boolean statement so a True becomes False and a False becomes True. The periodic_table_20 variable only contains information on the first twenty elements of the periodic table so the elements must be in either the s or p block. To determine whether silicon is in the s or the p block, two methods can be used:
if periodic_table_20['Si']['block'] == 's':
print("Silicon is in the s block.")
else:
print("Silicon is in the p block")
Alternatively, one could use a not statement such that:
if not(periodic_table_20['Si']['block'] == 's'):
print("Silicon is in the p block.")
else:
print("Silicon is in the s block")
Both are valid ways of determining whether silicon is in the s or p block. What is happening in the second method?
1) periodic_table_20['Si']['block'] == 's' is evaluated to False as silicon is not in the s block.
2) not(False) is evaluated to True.
3) if True: is evaluated and "Silicon is in the p block." is printed.
How does the process change if sodium is evaluated?
if not(periodic_table_20['Na']['block'] == 's'):
print("Sodium is in the p block.")
else:
print("Sodium is in the s block")
When sodium is evaluated the logic is:
Both are valid ways of determining whether silicon is in the s or p block. What is happening in the second method?
1) periodic_table_20['Na']['block'] == 's' is evaluated to True as sodium is in the s block.
2) not(True) is evaluated to False.
3) if False: is evaluated so the else statement is used and "Sodium is in the s block." is printed.
Exercise: Using a not statement determine whether calcium is in group 2.
## Write your code here
In the next tutorial loops will be introduced. The use of loops in combination with Boolean logic statements and flow controls can create efficient methods of analysing data.
