Types

Prerequisites

None

Types

Python essentially can be thought of as having three types of single object variable:

Strings - a textual variable, such as a word or a sentance
Numbers - some numerical information
Boolean - Boolean variables can be either True or False, this is an important component of logic

The particular type of variable defines the specific operations that may be performed on them. The type of any variable may be determined with the type() function (which is intrinsic to Python).

Strings

Strings (often abbrevated to str) are variables which are textual in nature. When assigning a string, the text should be placed between either inverted commas ('Like This') or quotation marks ("Like This"). This informs the Python interperator that the variable is of type str. For example, if we want to assign the string 'Hello World' to the variable greeting, the following code is used,

greeting = 'Hello World'

Printing this greeting (using the print() function) allows you to run the archetypical first programming exercise.

print(greeting)

Hello World

This exercise is often the first thing that is taught when learning a new programming language, so we feel that it is important, in this introductory text, that we show it.

type(greeting)

str

Note that as mentioned above, either inverted commas or quotation marks may be used so,

greeting2 = "Hello World"
print(greeting2)

Hello World

is equivalent to,

greeting = 'Hello World'
print(greeting)

Hello World

While strings are textual in nature, they may still contain numerical information.

hydrogen_atomic = "The atomic number (Z) of Hydrogen is 1. \n"
print(hydrogen_atomic)

The atomic number (Z) of Hydrogen is 1.

In the above example, the number 1 is a component of the string hydrogen and the \n means that a new line should be taken. This means that the Python interperator does not recognise it has a number so cannot perform mathematical operations (discussed below) on it.

Exercise

In the cell below, define a variable string containing your favourite chemical element (this is a chemistry textbook after all), and have the Python interpreter print it.

Operations

The textual nature of a string means that is it not possible (nor does it really make sense to) perform mathematical operations on them. However, there are some operations that can be performed on a string, that initially, may appear mathematical in nature. For examples, it is possible to "add" strings together,

hydrogen_mass = "The mass number (A) of Hydrogen is 1. "
print(hydrogen_atomic + hydrogen_mass)

The atomic number (Z) of Hydrogen is 1. 
The mass number (A) of Hydrogen is 1.

Here, the addition symbol (+) is used to concatenate the two strings, where the latter is appended to the end of the former. In mathematics, multiplication is analogous to multiple addition of a number, $$ 5 \times 3 = 5 + 5 + 5 = 15. $$ This analogy may be applied to the use of the multiplication symbol (in Python, *) as an operator on a string.

print(hydrogen_atomic * 3)

The atomic number (Z) of Hydrogen is 1. 
The atomic number (Z) of Hydrogen is 1. 
The atomic number (Z) of Hydrogen is 1.

Where, by "multiplying" the string by 3, we are concatenating three instances of the hydrogen_atomic variable.

If you attempt to subtract one string from another though, you will be met with an error message. Reading from the bottom, this error tells us that we have a TypeError: unsupported operand type(s) for -: 'str' and 'str' (more about errors and error messages can be found in Chapter X). This message says that it is not possible to subtract one string from another, this is because the - operator has no alternate meaning (like + means to concatenate) for strings.

print(hydrogen_atomic - hydrogen_mass)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-9-281ed67a144c> in <module>
----> 1 print(hydrogen_atomic - hydrogen_mass)

TypeError: unsupported operand type(s) for -: 'str' and 'str'

The same is the case for operating on a string with any of the other standard operators (division, floor division, and power) in Python.

Exercise

Test the other standard operations on a pair of strings in the cell below.

### Placeholder

Numbers

Numbers are a broad definition of a type in Python, indeed within numbers there are three other, more specific, data sub-types. Loosely, numbers are any numerical data in Python, and variable of this broad type are defined as follows,

chlorine_z = 17
print(chlorine_z)

triple_point_h2o = 273.16
print(triple_point_h2o)

273.16

Shown above are two of the three possible numerical types in Python. The first is the type int,

type(chlorine_z)

int

This is a whole number, a number without a decimal point (also known as an integer). The example shown above is the atomic number of chlorine, which is a whole number of 17 (a chlorine atom contains exactly 17 protons, any more or any less and it would be a different atom and it is not possible to have a 17.2 protons!). While the second example is of the type float,

type(triple_point_h2o)

float

This is a floating point number, a number with a decimal point. The given example is that of the triple point of water in units of Kelvin, which is not 273 K or 274 K, but rather lies somewhere in between on the number line.

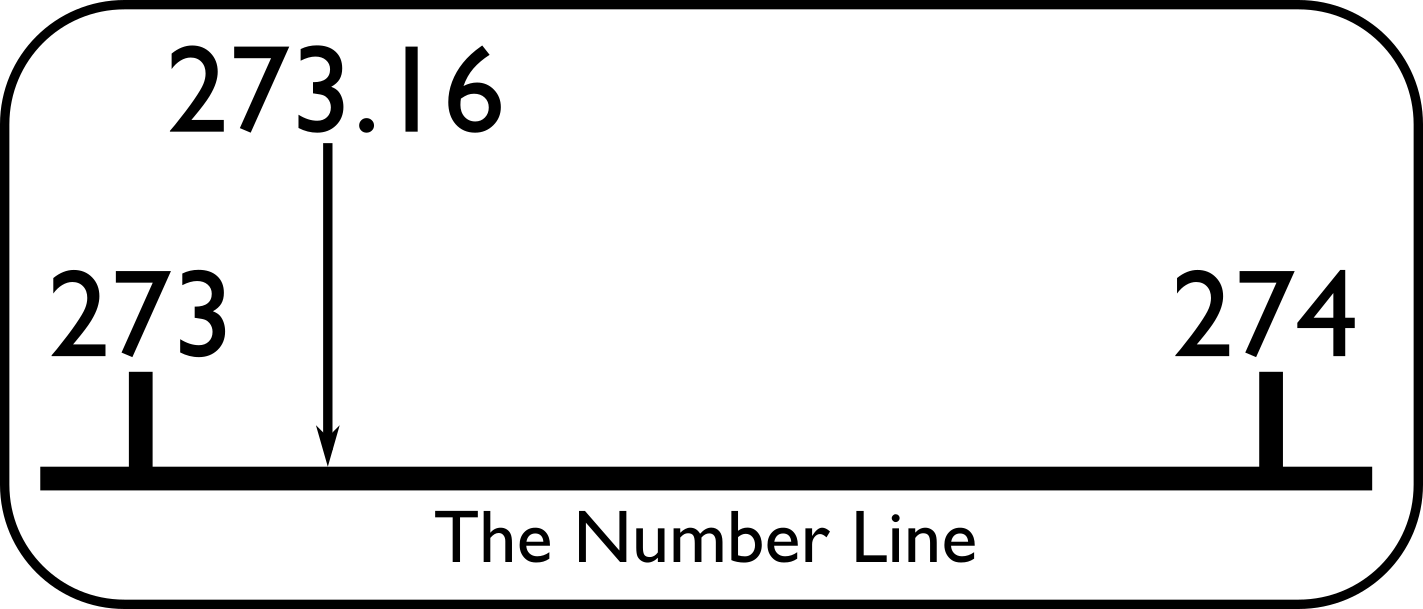
Figure 1. The position of 273.16 on the number line.

Floating point precision

Due to the way that the computer stores floating point numbers, you may notice some unusual results. For example (this may vary from computer to computer),

print(0.1 + 0.2)

0.30000000000000004

When run on my computer the above code returns 0.30000000000000004, which we know is not correct. This is due to the base 2 (ones and zeros, also known as binary) way that computers store information and the inability to represent 0.1 exactly in base 2. We make the assumption through this book, and generally, that the precision that the data is stored to is sufficient for our use cases. However, this may not always be the case so it is important to be aware of it!

Another way that floating point numbers may be represented, which can be useful in the physical sciences, is with scientific notation (also known as standard form). Python understands scientific notation as follow,

avogardo_constant = 6.022e23

where the coefficient of the standard notation value preceeds the e and the exponent follows. For example, you may be used to seeing Avogardo's constant written as,

$$ N_a = 6.022\times 10 ^{23}. $$

This way of defining a number will always produce a float type number, regardless of whether the decimal point is included or not.

type(avogardo_constant)

float

type(3e8)

float

Opertions

Python has five standard mathematical opertions that my be performed between variables of numerical data.

Table 1. The five standard mathematical operations that may be performed on numerical data.

Operation	Mathematical Notation	Pythonic Notation
Addition	$a + b$	`a + b`
Subtraction	$a - b$	`a - b`
Multiplicaton	$a \times b$	`a * b`
Division	$a \div b$	`a / b`
Exponent	$a ^ b$	`a ** b`

Each of these operations act exactly as you would expect.

print(3. + 2.)

5.0

print(3. - 2.)

1.0

print(3. * 2.)

6.0

print(3. / 2.)

1.5

print(3. ** 2.)

9.0

You may have noticed that in the five lines of code above, numbers of type float were used for all of them and the numbers that were returned were also of type float. These operations can also be used with numbers of type int.

print(3 + 2)

print(3 - 2)

print(3 * 2)

print(3 / 2)

1.5

print(3 ** 2)

Notice that all of the numbers that are returned are of type int, except for the result of 3 / 2, which the Python interperator has intelligently returned as a float (as the int 1 or 2 would not be correct). This is achieved by the division operator automatically upscaling all of its operands (the numbers that it operates on) to type float before the division is performed.

It was shown above that a number can be assigned to a variable, additionally this variable can then be used in a mathematical opertation. Consider converting from kilojoules to calories, where you divide by $4.184$.

kj = 100

calorie = 100 / 4.184

print(calorie)

23.900573613766728

Above, we have reused the kj variable in the creation of a new variable calorie and printed this.

Exercise

Investigate, in the cell below, the effect of changing the value of kj after the variable calorie is defined.

### Placeholder

Order of operations

A single line of Python can contain many different mathematical operations, therefore it is important that Python has an order in which these operations should be performed. This is the standard mathematical order of operations, this is known as many things (PIMDAS, POMDAS, BIDMAS, etc.). However, we will refer to this as BODMAS:

Brackets
Order
Division
Multiplication
Addition
Subtraction

Exercise

Write the following equations in the cells below, before you returns them use a calculator and BODMAS to determine what the answer should be.

$3 \div (4 + 2) \times 3$
$8 + 9 \times 7 ^ 3$

### Placeholder

### Placeholder

Complex numbers

Many chemistry students (and chemistry educators!) ignore the importance of complex numbers in the chemical sciences. However, there are many aspects where complex numbers are relavent, such as the amount by which an X-ray is scattered by an atom and the evalution of the wavefunction in quantum mechanics. Therefore, it is important that we (briefly) discuss complex numbers and how to use them in Python.

Typically, we would expect a complex number to be written as $3 + 1i$, where the number has a real component of 3 and a complex component of 1. In Python, a j is used instead of an $i$, this is due to Python following a convention in electrical engineering where the complex component is denoted with a $j$. Therefore, to write the complex number mentioned earlier ($3 + 1i$) would be the following,

print(3 + 1j)

(3+1j)

type(3 + 1j)

complex

Mixed type operations and type hierarchy

The upscaling of types does not only happen for the division operator, it will also occur when two objects of different types are operated on. For example, consider what would happen if an int is added to a float,

print(1.5 + 2)

3.5

type(1.5 + 2)

float

The result is a float, this is because the int is upscaled to be a float before the addition is performed. Essentially what the computer sees is,

>>> 1.5 + 2      # float plus int
>>> 1.5 + 2.0    # Upscale int to float
>>> 3.5          # Do addition

This is the case for any mathematical operation between a float and an int.

In order for the upscaling to make sense, a hierarchy of types must be defined. In Python for numerical variables this is as follows:

complex
float
int

So an int will upscale to a float and a float to a complex.

Boolean

The final type in Python that we will discuss in this section is the Boolean, named for George Boole who defined an early algebraic system of logic in the 19th century (which is fundamental to modern computer science). The Boolean or bool type is a logical variable type, meaning that it is associated with computational logic. A bool can take one of two values, either True or False.

print(True)

True

type(False)

bool

Note that in Python, it is important that these are write exactly as shown above (in title case), or an error will be thrown.

print(true)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-37-d6f700e50a15> in <module>
----> 1 print(true)

NameError: name 'true' is not defined

Logical operators

The utility of bool types is due to their application in logic, where it is possible to determine if a particular statement is True or False. For example, the == operator determines if the item on the left is equal to that on the right.

2 + 2 == 4

True

3 + 1 == -4

False

Of course, == is not the only logical operator.

Table 2. The six standard logical operations that may be performed.

Operation	Mathematical Notation	Pythonic Notation
Is Equal To	$=$	`==`
Less Than	$<$	`<`
Less Than or Equal to	$\leq$	`<=`
Greater Than	$>$	`>`
Greater Than or Equal to	$\geq$	`>=`
Is Not Equal to	$\neq$	`!=`

Each of these operators has the same effect as their mathematical equivalent when applied to numerical data. However, some of these operators are not limited to numerical data. For example, the == and != may be used for any data type,

'Hello World' != 'HELLO WORLD'

True

# The .upper() class-function will make the string uppercase
'Hello World'.upper() == 'HELLO WORLD'

True

Exercise

Using the cells below, find the result of the following logical operations:

$1 = 4$
$10 < 15$
$3.1415 \neq 3$

### Placeholder

### Placeholder

### Placeholder