Model Complexity and the Goal of Fitting

When developing models, it is important to understand that our goal is not to find a function that exactly reproduces our experimental measurements. Any real experiment includes some random measurement error, and a model that perfectly fits such data would be fitting not just the underlying relationship but also this experimental noise. More importantly, such a perfect fit would likely fail to capture the general relationship that we are actually interested in understanding.

Instead, we seek a model that captures the essential relationship between our variables while being general enough to make useful predictions about new measurements. Think of fitting a calibration curve: while we could force our model through every calibration point exactly, we are usually more interested in a smooth curve that represents the general trend. This smoother curve might not pass exactly through any individual point, but it is likely to give us better predictions when we use it for future measurements.

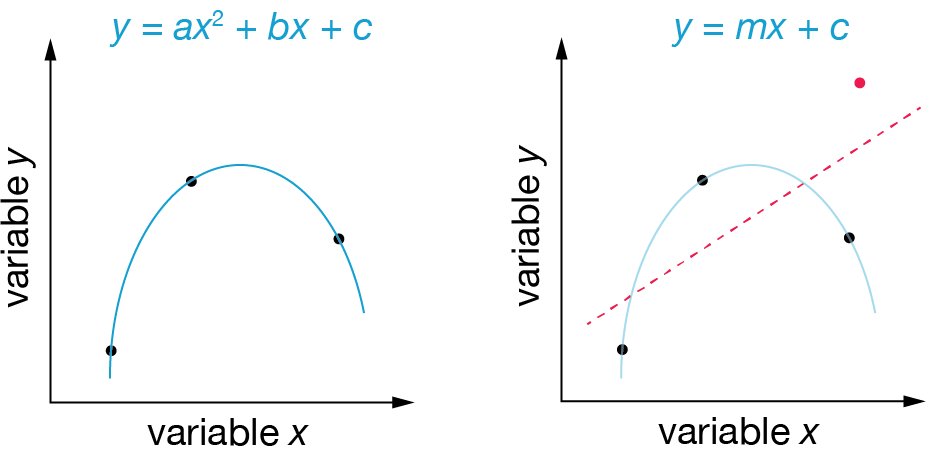
Fig. 4 Choosing model complexity: Two possible fits to the same data points (black dots). The quadratic model (left) perfectly fits all three points but implies a specific curving behavior that may not represent the true relationship. The linear model (right) does not pass exactly through the points but might better capture the underlying trend. The observation of an additional data point (red) suggests the simpler linear model would have been more appropriate.

This brings us to an important balance between model complexity and utility. A more complex model (like a high-degree polynomial) can always fit our data points more closely than a simpler model. However, this apparent improvement in fit can be misleading. Complex models can end up fitting not just the true underlying relationship but also the random noise in our measurements — a problem known as overfitting.

Gnerally, we prefer simpler models unless we have good reason to use a more complex one. A simple model that captures the main trends in our data is often more useful than a complex one that fits every point perfectly but fails to generalize to new measurements.