Finding the Best Fit

Once we have chosen our model’s functional form, we need a systematic way to find the best parameter values. A common way to do this is to choose a metric that defines our “quality of fit” and then choose parameter values that optimise this metric.

One approach is to consider the “residuals” we obtain for a given set of parameter values — these are the differenes between our model’s predicted \(y\) values and the \(y\) values of the observed data. We then compute our “quality of fit” metric from these residuals.

A popular quality-of-fit metric is the sum of the squares of the residuals:

\[\chi^2 = \sum_i \left[y_i^\mathrm{data} - y_i^\mathrm{model}\right]^2\]

If we are fitting a linear model (also called “linear regression”), this choice of metric gives us a “least-squares” fit.

For least-squares linear regression, the values of \(m\) and \(c\) that minimise \(\chi^2\) can be calculated directly from an analytical solution. However, for more complex models, we typically need to use numerical optimization methods to find the optimal parameter values. This is where computational methods become essential — we can use algorithms like those in scipy.optimize.minimize() to numerically search for the best-fit parameters.

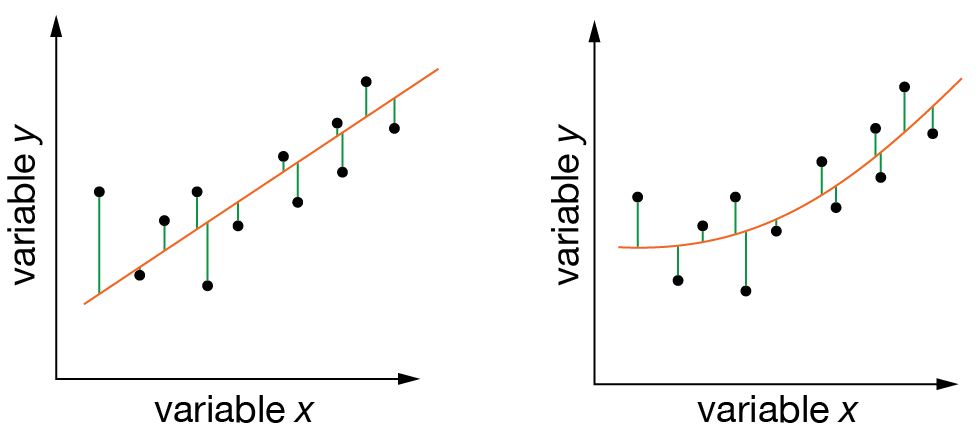
Fig. 5 Calculating the quality of fit for two different models. (Left) Fitting a linear model. (Right) Fitting a non-linear model. In each case, we find the best-fit parameters by minimising the sum of squared residuals (green lines).