Worked Examples: Gradient Descent Method#
These worked solutions correspond to the exercises on the Gradient Descent Method page.
How to use this notebook:
Try each exercise yourself first before looking at the solution
The code cells show both the code and its output
Download this notebook if you want to run and experiment with the code yourself
Your solution might look different - that’s fine as long as it gives the correct answer!
Exercise: Fixed Step Size Gradient Descent#
Problem: Implement gradient descent with a fixed step size to find the minimum of the harmonic potential energy surface. We need to first write a function to calculate the first derivative of the harmonic potential:
Then implement the gradient descent algorithm using:
We’ll start from \(r = 1.0\) Å and explore how different step sizes affect convergence.
Setup: Define functions#
First, we’ll define our harmonic potential and its derivative:
import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format='retina'
def harmonic_potential(r, k, r_0):
"""Calculate the harmonic potential energy.
Args:
r (float): Bond length (Å). Can be a float or np.ndarray.
k (float): Force constant (eV Å^-2).
r_0 (float): Equilibrium bond length (Å).
Returns:
Potential energy (eV). Type matches input r.
"""
return 0.5 * k * (r - r_0) ** 2
def harmonic_gradient(r, k, r_0):
"""Calculate the first derivative of the harmonic potential.
Args:
rr (float): Bond length (Å). Can be a float or np.ndarray.
k (float): Force constant (eV Å^-2).
r_0 (float): Equilibrium bond length (Å).
Returns:
First derivative dU/dr (eV Å^-1). Type matches input r.
"""
return k * (r - r_0)
# Parameters for H₂
k = 36.0 # eV Å^-2
r_0 = 0.74 # Å
# Test the gradient function
r_test = 1.0 # Å
gradient = harmonic_gradient(r_test, k, r_0)
print(f"Gradient at r = {r_test} Å: U'(r) = {gradient:.3f} eV Å^-1")
Gradient at r = 1.0 Å: U'(r) = 9.360 eV Å^-1
Part 1: Fixed step size Δr = 0.01 Å#
Let’s implement the gradient descent algorithm with a small step size and see how it performs:
# Gradient descent parameters
r_start = 1.0 # Å
delta_r = 0.01 # Å (step size)
max_iterations = 50
convergence_threshold = 0.001 # eV Å⁻¹
# Initialize
r_current = r_start
r_history = [r_current]
gradient_history = []
print(f"Starting gradient descent with Δr = {delta_r} Å\n")
print("Iteration | Position (Å) | Gradient (eV Å⁻¹)")
print("-" * 50)
converged = False
for iteration in range(max_iterations):
# Calculate gradient at current position
gradient = harmonic_gradient(r_current, k, r_0)
gradient_history.append(gradient)
print(f"{iteration:9d} | {r_current:12.6f} | {gradient:18.6f}")
# Check for convergence
if abs(gradient) < convergence_threshold:
print(f"\nConverged after {iteration} iterations!")
print(f"Final position: r = {r_current:.6f} Å")
print(f"Analytical solution: r₀ = {r_0} Å")
print(f"Error: {abs(r_current - r_0):.6f} Å")
converged = True
break
# Update position (gradient descent step)
r_current = r_current - delta_r * np.sign(gradient)
r_history.append(r_current)
if not converged:
print(f"\nDid not converge within {max_iterations} iterations.")
print(f"Final position: r = {r_current:.6f} Å")
print(f"Final gradient: {gradient:.6f} eV Å⁻¹")
Starting gradient descent with Δr = 0.01 Å
Iteration | Position (Å) | Gradient (eV Å⁻¹)
--------------------------------------------------
0 | 1.000000 | 9.360000
1 | 0.990000 | 9.000000
2 | 0.980000 | 8.640000
3 | 0.970000 | 8.280000
4 | 0.960000 | 7.920000
5 | 0.950000 | 7.560000
6 | 0.940000 | 7.200000
7 | 0.930000 | 6.840000
8 | 0.920000 | 6.480000
9 | 0.910000 | 6.120000
10 | 0.900000 | 5.760000
11 | 0.890000 | 5.400000
12 | 0.880000 | 5.040000
13 | 0.870000 | 4.680000
14 | 0.860000 | 4.320000
15 | 0.850000 | 3.960000
16 | 0.840000 | 3.600000
17 | 0.830000 | 3.240000
18 | 0.820000 | 2.880000
19 | 0.810000 | 2.520000
20 | 0.800000 | 2.160000
21 | 0.790000 | 1.800000
22 | 0.780000 | 1.440000
23 | 0.770000 | 1.080000
24 | 0.760000 | 0.720000
25 | 0.750000 | 0.360000
26 | 0.740000 | -0.000000
Converged after 26 iterations!
Final position: r = 0.740000 Å
Analytical solution: r₀ = 0.74 Å
Error: 0.000000 Å
Explanation:
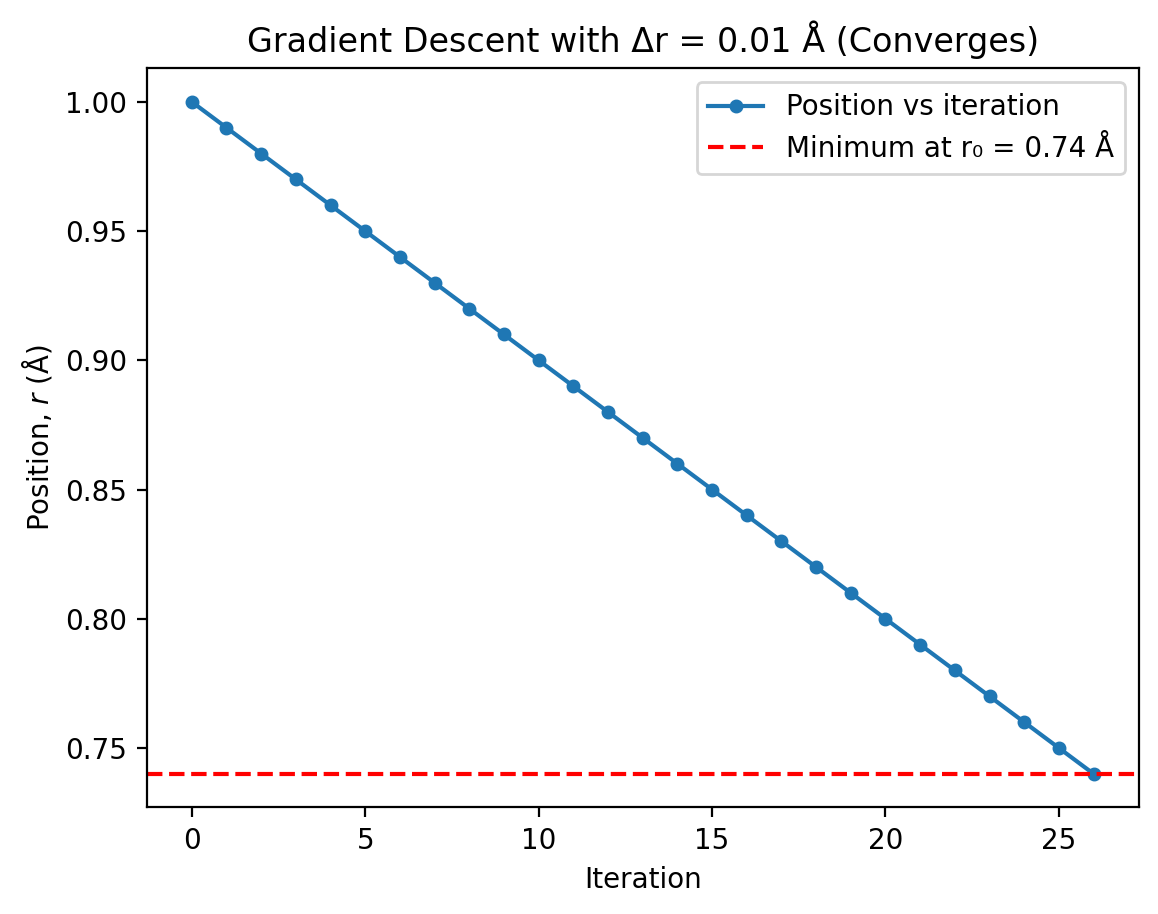
With \(\Delta r = 0.01\) Å, the algorithm converges successfully in 26 iterations. Key observations:
Steady convergence: The position moves consistently towards the minimum at \(r_0 = 0.74\) Å.
Fixed step size: Each iteration moves exactly 0.01 Å in the direction indicated by the gradient sign:
When \(r > r_0\): gradient is positive, so we step left (decrease \(r\))
When \(r < r_0\): gradient is negative, so we step right (increase \(r\))
Final accuracy: The algorithm stops when \(|U'(r)| < 0.001\) eV Å⁻¹, which occurs at approximately \(r = 0.74\) Å—exactly the analytical minimum!
Why 26 iterations?: Starting at \(r = 1.0\) Å, we need to travel \(0.26\) Å to reach \(r_0 = 0.74\) Å. With steps of 0.01 Å, this requires about \(0.26 / 0.01 = 26\) steps.
The method is straightforward but slow—each small step requires a function evaluation.
Part 2: Fixed step size Δr = 0.1 Å#
Now let’s try a larger step size to see if we can converge faster:
# Try larger step size
r_start = 1.0 # Å
delta_r = 0.1 # Å (larger step size)
max_iterations = 50
convergence_threshold = 0.001 # eV Å⁻¹
# Initialize
r_current = r_start
r_history_large = [r_current]
gradient_history_large = []
print(f"Starting gradient descent with Δr = {delta_r} Å\n")
print("Iteration | Position (Å) | Gradient (eV Å⁻¹)")
print("-" * 50)
converged = False
for iteration in range(max_iterations):
# Calculate gradient at current position
gradient = harmonic_gradient(r_current, k, r_0)
gradient_history_large.append(gradient)
print(f"{iteration:9d} | {r_current:12.6f} | {gradient:18.6f}")
# Check for convergence
if abs(gradient) < convergence_threshold:
print(f"\nConverged after {iteration} iterations!")
print(f"Final position: r = {r_current:.6f} Å")
converged = True
break
# Update position
r_current = r_current - delta_r * np.sign(gradient)
r_history_large.append(r_current)
if not converged:
print(f"\nDid not converge within {max_iterations} iterations.")
Starting gradient descent with Δr = 0.1 Å
Iteration | Position (Å) | Gradient (eV Å⁻¹)
--------------------------------------------------
0 | 1.000000 | 9.360000
1 | 0.900000 | 5.760000
2 | 0.800000 | 2.160000
3 | 0.700000 | -1.440000
4 | 0.800000 | 2.160000
5 | 0.700000 | -1.440000
6 | 0.800000 | 2.160000
7 | 0.700000 | -1.440000
8 | 0.800000 | 2.160000
9 | 0.700000 | -1.440000
10 | 0.800000 | 2.160000
11 | 0.700000 | -1.440000
12 | 0.800000 | 2.160000
13 | 0.700000 | -1.440000
14 | 0.800000 | 2.160000
15 | 0.700000 | -1.440000
16 | 0.800000 | 2.160000
17 | 0.700000 | -1.440000
18 | 0.800000 | 2.160000
19 | 0.700000 | -1.440000
20 | 0.800000 | 2.160000
21 | 0.700000 | -1.440000
22 | 0.800000 | 2.160000
23 | 0.700000 | -1.440000
24 | 0.800000 | 2.160000
25 | 0.700000 | -1.440000
26 | 0.800000 | 2.160000
27 | 0.700000 | -1.440000
28 | 0.800000 | 2.160000
29 | 0.700000 | -1.440000
30 | 0.800000 | 2.160000
31 | 0.700000 | -1.440000
32 | 0.800000 | 2.160000
33 | 0.700000 | -1.440000
34 | 0.800000 | 2.160000
35 | 0.700000 | -1.440000
36 | 0.800000 | 2.160000
37 | 0.700000 | -1.440000
38 | 0.800000 | 2.160000
39 | 0.700000 | -1.440000
40 | 0.800000 | 2.160000
41 | 0.700000 | -1.440000
42 | 0.800000 | 2.160000
43 | 0.700000 | -1.440000
44 | 0.800000 | 2.160000
45 | 0.700000 | -1.440000
46 | 0.800000 | 2.160000
47 | 0.700000 | -1.440000
48 | 0.800000 | 2.160000
49 | 0.700000 | -1.440000
Did not converge within 50 iterations.
Explanation:
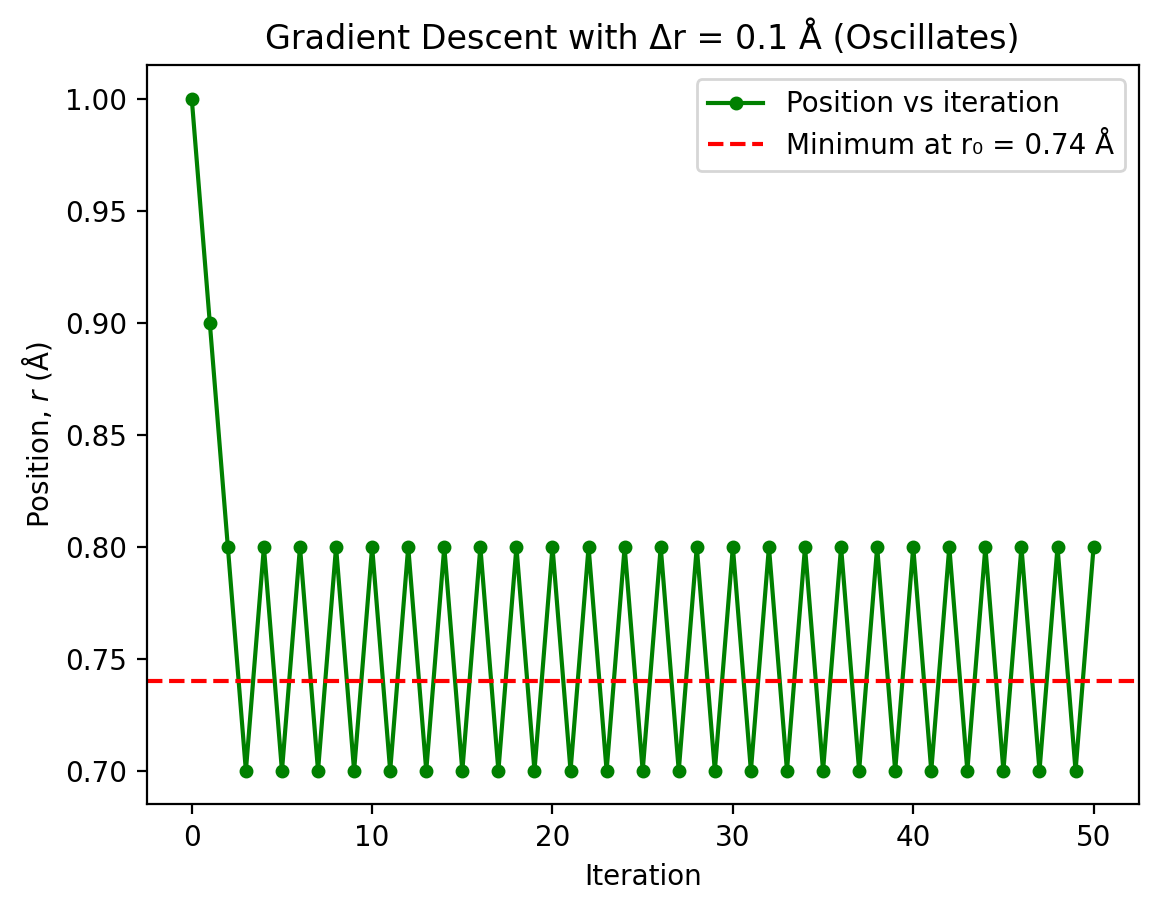
With \(\Delta r = 0.1\) Å, the algorithm fails to converge and instead oscillates around the minimum. Here’s why:
Overshooting: Starting at \(r = 1.0\) Å, the minimum is at \(r_0 = 0.74\) Å, a distance of only 0.26 Å. A step size of 0.1 Å is too large relative to this distance.
The oscillation pattern:
Iteration 0: \(r = 1.0\) Å → gradient positive → step left
Iteration 1: \(r = 0.9\) Å (overshot to the left side of minimum)
Iteration 2: \(r = 0.8\) Å (gradient now negative, step right)
Iteration 3: \(r = 0.9\) Å (back to the right side)
The algorithm bounces back and forth between \(r = 0.8\) Å and \(r = 0.9\) Å
Why no convergence?: The fixed 0.1 Å steps are too large to “land” close enough to the minimum where \(|U'(r)| < 0.001\) eV Å⁻¹. The algorithm perpetually overshoots.
This demonstrates a fundamental limitation of fixed step size gradient descent: the step size must be carefully chosen, and what works for one starting position may not work for another.
Visualizing the oscillation#
Let’s plot both convergence paths to see the difference clearly:
# First, recreate the successful run with small step size for plotting
r_current = 1.0
r_history_small = [r_current]
delta_r_small = 0.01
for iteration in range(26):
gradient = harmonic_gradient(r_current, k, r_0)
if abs(gradient) < 0.001:
break
r_current = r_current - delta_r_small * np.sign(gradient)
r_history_small.append(r_current)
# Plot the small step size (converges)
plt.plot(r_history_small, 'o-', markersize=4, linewidth=1.5, label='Position vs iteration')
plt.axhline(r_0, color='r', linestyle='--', label=f'Minimum at r₀ = {r_0} Å')
plt.xlabel('Iteration')
plt.ylabel('Position, $r$ (Å)')
plt.title(f'Gradient Descent with Δr = 0.01 Å (Converges)')
plt.legend()
plt.show()
# Plot the large step size (oscillates)
plt.plot(r_history_large, 'go-', markersize=4,
label='Position vs iteration')
plt.axhline(r_0, color='r', linestyle='--', label=f'Minimum at r₀ = {r_0} Å')
plt.xlabel('Iteration')
plt.ylabel('Position, $r$ (Å)')
plt.title(f'Gradient Descent with Δr = 0.1 Å (Oscillates)')
plt.legend()
plt.show()
Exercise: Adaptive Step Size Gradient Descent#
The fixed step size method showed us that choosing an appropriate step size is crucial but difficult. An adaptive approach rescales the step size based on the local gradient magnitude:
where \(\alpha\) is the learning rate parameter. This approach naturally takes smaller steps near the minimum (where the gradient is small) and larger steps far from the minimum (where the gradient is large).
Part 1: Learning rate α = 0.01#
Let’s implement adaptive step size gradient descent:
def gradient_descent_adaptive(r_start, alpha, k, r_0, max_iterations=50, threshold=0.001):
"""Perform adaptive step size gradient descent.
Args:
r_start (float): Starting position (Å).
alpha (float): Learning rate.
k (float): Force constant (eV Å⁻²).
r_0 (float): Equilibrium bond length (Å).
max_iterations (int): Maximum number of iterations.
threshold (float): Convergence threshold for |gradient|.
Returns:
tuple: (r_history, gradient_history, converged, num_iterations).
"""
r_current = r_start
r_history = [r_current]
gradient_history = []
print(f"\nAdaptive gradient descent with α = {alpha}\n")
print("Iteration | Position (Å) | Gradient (eV Å⁻¹) | Δr (Å)")
print("-" * 65)
converged = False
for iteration in range(max_iterations):
# Calculate gradient
gradient = harmonic_gradient(r_current, k, r_0)
gradient_history.append(gradient)
# Calculate step size (adaptive)
step = -alpha * gradient
print(f"{iteration:9d} | {r_current:12.6f} | {gradient:17.6f} | {step:9.6f}")
# Check convergence
if abs(gradient) < threshold:
print(f"\nConverged after {iteration} iterations!")
print(f"Final position: r = {r_current:.6f} Å")
print(f"Analytical solution: r_0 = {r_0} Å")
print(f"Error: {abs(r_current - r_0):.6f} Å")
converged = True
break
# Update position
r_current = r_current + step
r_history.append(r_current)
if not converged:
print(f"\nDid not converge within {max_iterations} iterations.")
return r_history, gradient_history, converged, iteration
# Run with α = 0.01
r_history_01, grad_history_01, converged_01, iters_01 = gradient_descent_adaptive(
1.0, 0.01, k, r_0
)
Adaptive gradient descent with α = 0.01
Iteration | Position (Å) | Gradient (eV Å⁻¹) | Δr (Å)
-----------------------------------------------------------------
0 | 1.000000 | 9.360000 | -0.093600
1 | 0.906400 | 5.990400 | -0.059904
2 | 0.846496 | 3.833856 | -0.038339
3 | 0.808157 | 2.453668 | -0.024537
4 | 0.783621 | 1.570347 | -0.015703
5 | 0.767917 | 1.005022 | -0.010050
6 | 0.757867 | 0.643214 | -0.006432
7 | 0.751435 | 0.411657 | -0.004117
8 | 0.747318 | 0.263461 | -0.002635
9 | 0.744684 | 0.168615 | -0.001686
10 | 0.742998 | 0.107913 | -0.001079
11 | 0.741918 | 0.069065 | -0.000691
12 | 0.741228 | 0.044201 | -0.000442
13 | 0.740786 | 0.028289 | -0.000283
14 | 0.740503 | 0.018105 | -0.000181
15 | 0.740322 | 0.011587 | -0.000116
16 | 0.740206 | 0.007416 | -0.000074
17 | 0.740132 | 0.004746 | -0.000047
18 | 0.740084 | 0.003037 | -0.000030
19 | 0.740054 | 0.001944 | -0.000019
20 | 0.740035 | 0.001244 | -0.000012
21 | 0.740022 | 0.000796 | -0.000008
Converged after 21 iterations!
Final position: r = 0.740022 Å
Analytical solution: r_0 = 0.74 Å
Error: 0.000022 Å
Explanation:
With \(\alpha = 0.01\), the algorithm converges successfully. Let’s examine how the adaptive step sizes work:
Key observations:
Adaptive step sizes: Notice how the “Δr (Å)” column changes:
Early iterations: When far from the minimum, the gradient is large (e.g., 9.36 eV Å−1 initially), so steps are large (−0.0936 Å)
Later iterations: As we approach the minimum, the gradient decreases, and steps become progressively smaller
Near convergence: Steps become very small as the gradient approaches zero
Natural damping: The step size automatically decreases as we approach the minimum because the gradient magnitude decreases. This prevents oscillation.
Efficiency: The adaptive method allows large initial steps when far from the minimum, then automatically refines with smaller steps near convergence, without needing to manually tune the step size.
Why it works: For the harmonic potential, \(U'(r) = k(r - r_0)\), so the gradient is directly proportional to the distance from the minimum. The adaptive step size therefore automatically scales with this distance.
Part 2: Learning rate α = 0.001#
What happens with a smaller learning rate?
# Run with α = 0.001 (smaller)
r_history_001, grad_history_001, converged_001, iters_001 = gradient_descent_adaptive(
1.0, 0.001, k, r_0
)
Adaptive gradient descent with α = 0.001
Iteration | Position (Å) | Gradient (eV Å⁻¹) | Δr (Å)
-----------------------------------------------------------------
0 | 1.000000 | 9.360000 | -0.009360
1 | 0.990640 | 9.023040 | -0.009023
2 | 0.981617 | 8.698211 | -0.008698
3 | 0.972919 | 8.385075 | -0.008385
4 | 0.964534 | 8.083212 | -0.008083
5 | 0.956450 | 7.792217 | -0.007792
6 | 0.948658 | 7.511697 | -0.007512
7 | 0.941147 | 7.241276 | -0.007241
8 | 0.933905 | 6.980590 | -0.006981
9 | 0.926925 | 6.729289 | -0.006729
10 | 0.920195 | 6.487034 | -0.006487
11 | 0.913708 | 6.253501 | -0.006254
12 | 0.907455 | 6.028375 | -0.006028
13 | 0.901426 | 5.811353 | -0.005811
14 | 0.895615 | 5.602145 | -0.005602
15 | 0.890013 | 5.400468 | -0.005400
16 | 0.884613 | 5.206051 | -0.005206
17 | 0.879406 | 5.018633 | -0.005019
18 | 0.874388 | 4.837962 | -0.004838
19 | 0.869550 | 4.663795 | -0.004664
20 | 0.864886 | 4.495899 | -0.004496
21 | 0.860390 | 4.334046 | -0.004334
22 | 0.856056 | 4.178021 | -0.004178
23 | 0.851878 | 4.027612 | -0.004028
24 | 0.847850 | 3.882618 | -0.003883
25 | 0.843968 | 3.742844 | -0.003743
26 | 0.840225 | 3.608101 | -0.003608
27 | 0.836617 | 3.478210 | -0.003478
28 | 0.833139 | 3.352994 | -0.003353
29 | 0.829786 | 3.232286 | -0.003232
30 | 0.826553 | 3.115924 | -0.003116
31 | 0.823438 | 3.003751 | -0.003004
32 | 0.820434 | 2.895616 | -0.002896
33 | 0.817538 | 2.791374 | -0.002791
34 | 0.814747 | 2.690884 | -0.002691
35 | 0.812056 | 2.594012 | -0.002594
36 | 0.809462 | 2.500628 | -0.002501
37 | 0.806961 | 2.410605 | -0.002411
38 | 0.804551 | 2.323823 | -0.002324
39 | 0.802227 | 2.240166 | -0.002240
40 | 0.799987 | 2.159520 | -0.002160
41 | 0.797827 | 2.081777 | -0.002082
42 | 0.795745 | 2.006833 | -0.002007
43 | 0.793739 | 1.934587 | -0.001935
44 | 0.791804 | 1.864942 | -0.001865
45 | 0.789939 | 1.797804 | -0.001798
46 | 0.788141 | 1.733083 | -0.001733
47 | 0.786408 | 1.670692 | -0.001671
48 | 0.784737 | 1.610547 | -0.001611
49 | 0.783127 | 1.552568 | -0.001553
Did not converge within 50 iterations.
Explanation:
With \(\alpha = 0.001\), the algorithm does not converge within 50 iterations. After 49 iterations, the gradient is still 1.55 eV Å⁻¹, well above the convergence threshold of 0.001 eV Å⁻¹.
The problem:
Too conservative: With such a small learning rate, each step is very cautious:
Iteration 0: Step is only −0.00936 Å (compared to −0.0936 Å with \(\alpha = 0.01\))
After 49 iterations, we’ve only reached \(r = 0.783\) Å, still 0.043 Å away from the minimum at \(r_0 = 0.74\) Å
Progress is too slow: The gradient decreases very gradually from 9.36 eV Å⁻¹ to 1.55 eV Å⁻¹, but we’re making progress at such a slow rate that we can’t reach convergence.
Many more iterations needed: To converge with this learning rate would require several hundred iterations.
The learning rate is too small: Whilst smaller learning rates are more stable (less likely to diverge), if they’re too small, convergence becomes impractically slow. This learning rate of 0.001 is simply too conservative for efficient optimisation.
Part 3: Learning rate α = 0.1#
What happens with a larger learning rate?
# Run with α = 0.1 (larger)
r_history_1, grad_history_1, converged_1, iters_1 = gradient_descent_adaptive(
1.0, 0.1, k, r_0, max_iterations=50
)
Adaptive gradient descent with α = 0.1
Iteration | Position (Å) | Gradient (eV Å⁻¹) | Δr (Å)
-----------------------------------------------------------------
0 | 1.000000 | 9.360000 | -0.936000
1 | 0.064000 | -24.336000 | 2.433600
2 | 2.497600 | 63.273600 | -6.327360
3 | -3.829760 | -164.511360 | 16.451136
4 | 12.621376 | 427.729536 | -42.772954
5 | -30.151578 | -1112.096794 | 111.209679
6 | 81.058102 | 2891.451663 | -289.145166
7 | -208.087065 | -7517.774325 | 751.777432
8 | 543.690368 | 19546.213244 | -1954.621324
9 | -1410.930957 | -50820.154435 | 5082.015444
10 | 3671.084487 | 132132.401532 | -13213.240153
11 | -9542.155666 | -343544.243982 | 34354.424398
12 | 24812.268732 | 893215.034353 | -89321.503435
13 | -64509.234703 | -2322359.089319 | 232235.908932
14 | 167726.674229 | 6038133.632229 | -603813.363223
15 | -436086.688994 | -15699147.443794 | 1569914.744379
16 | 1133828.055385 | 40817783.353866 | -4081778.335387
17 | -2947950.280001 | -106126236.720050 | 10612623.672005
18 | 7664673.392004 | 275928215.472131 | -27592821.547213
19 | -19928148.155209 | -717413360.227540 | 71741336.022754
20 | 51813187.867545 | 1865274736.591605 | -186527473.659161
21 | -134714285.791616 | -4849714315.138174 | 484971431.513817
22 | 350257145.722201 | 12609257219.359253 | -1260925721.935925
23 | -910668576.213724 | -32784068770.334057 | 3278406877.033406
24 | 2367738300.819682 | 85238578802.868561 | -8523857880.286857
25 | -6156119579.467175 | -221620304887.458282 | 22162030488.745831
26 | 16005910909.278656 | 576212792707.391602 | -57621279270.739166
27 | -41615368361.460510 | -1498153261039.218262 | 149815326103.921844
28 | 108199957742.461334 | 3895198478701.967773 | -389519847870.196777
29 | -281319890127.735474 | -10127516044625.117188 | 1012751604462.511719
30 | 731431714334.776245 | 26331541716025.304688 | -2633154171602.530762
31 | -1901722457267.754395 | -68462008461665.796875 | 6846200846166.580078
32 | 4944478388898.826172 | 178001222000331.093750 | -17800122200033.109375
33 | -12855643811134.283203 | -462803177200860.875000 | 46280317720086.093750
34 | 33424673908951.812500 | 1203288260722238.750000 | -120328826072223.875000
35 | -86904152163272.062500 | -3128549477877820.500000 | 312854947787782.062500
36 | 225950795624510.000000 | 8134228642482333.000000 | -813422864248233.375000
37 | -587472068623723.375000 | -21148994470454068.000000 | 2114899447045407.000000
38 | 1527427378421683.500000 | 54987385623180576.000000 | -5498738562318058.000000
39 | -3971311183896374.500000 | -142967202620269504.000000 | 14296720262026952.000000
40 | 10325409078130578.000000 | 371714726812700800.000000 | -37171472681270080.000000
41 | -26846063603139504.000000 | -966458289713022208.000000 | 96645828971302224.000000
42 | 69799765368162720.000000 | 2512791553253857792.000000 | -251279155325385792.000000
43 | -181479389957223072.000000 | -6533258038460030976.000000 | 653325803846003072.000000
44 | 471846413888780032.000000 | 16986470899996082176.000000 | -1698647089999608320.000000
45 | -1226800676110828288.000000 | -44164824339989815296.000000 | 4416482433998981632.000000
46 | 3189681757888153600.000000 | 114828543283973521408.000000 | -11482854328397352960.000000
47 | -8293172570509199360.000000 | -298554212538331168768.000000 | 29855421253833117696.000000
48 | 21562248683323916288.000000 | 776240952599660986368.000000 | -77624095259966095360.000000
49 | -56061846576642179072.000000 | -2018226476759118512128.000000 | 201822647675911864320.000000
Did not converge within 50 iterations.
Explanation:
With \(\alpha = 0.1\), the algorithm diverges! The position oscillates with increasing amplitude and never converges.
Why this happens:
Overcorrection: The first step is: $\(\Delta r_0 = -\alpha U'(r_0) = -0.1 \times 9.36 = -0.936 \text{ Å}\)\( This moves from \)r = 1.0\( Å to \)r = 0.064\( Å, overshooting the minimum at \)r_0 = 0.74$ Å by a large margin.
Growing oscillations: Each subsequent step overshoots even more dramatically:
The gradient on the far side of the minimum has opposite sign and large magnitude
The large \(\alpha\) amplifies this, causing increasingly wild swings
The position alternates sides but moves further from the minimum each time
Instability criterion: For the harmonic potential with \(U'(r) = k(r - r_0)\), the algorithm is stable when: $\(\alpha < \frac{2}{k}\)\( For our case with \)k = 36.0\( eV Å⁻²: \)\(\alpha < \frac{2}{36} \approx 0.056\)\( Our \)\alpha = 0.1$ exceeds this threshold, causing divergence.
This demonstrates that whilst adaptive step sizes help, the learning rate parameter must still be chosen carefully. Too small and convergence is slow; too large and the algorithm diverges.
Summary: Choosing the learning rate#
Adaptive vs. fixed: Adaptive step sizes (\(r_{i+1} = r_i - \alpha U'(r_i)\)) can outperform fixed step sizes because they automatically adjust based on proximity to the minimum.
The learning rate determines convergence speed: There’s a “sweet spot” for \(\alpha\):
Too small: stable but slow
Just right: fast convergence
Too large: divergence
Problem-specific tuning: The optimal \(\alpha\) depends on the problem (specifically, the curvature \(k\) for harmonic potentials). For different force constants, different learning rates would be optimal.