Exercises

Exercises#

First, we must create NumPy arrays to storage each of the three columns of data in the table.

import numpy as np

p = np.array([5020, 60370, 20110, 46940, 362160])
V = np.array([0.8, 0.2, 1.0, 0.6, 0.1])
T = np.array([200, 600, 1000, 1400, 1800])

Now we plot, \(p\) against \(T\).

import matplotlib.pyplot as plt

plt.plot(T, p, 'o')
plt.xlabel('$T$')
plt.ylabel('$p$')
plt.show()
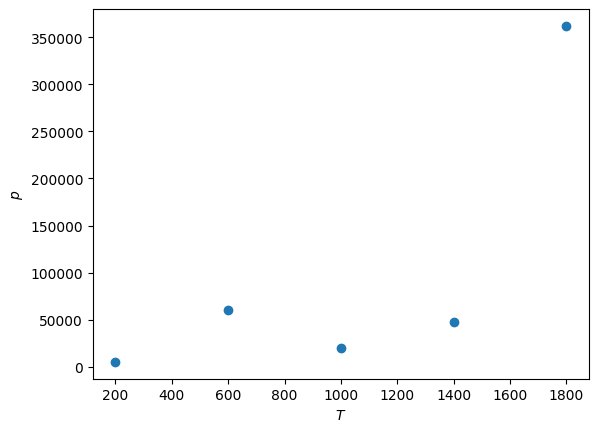
../_images/2969582c567c42ce0515f06a7b616a67ac87b70ed93a5c00bfacea0643c260c1.png

Then \(V\) against \(T\)

plt.plot(T, V, 'o')
plt.xlabel('$T$')
plt.ylabel('$V$')
plt.show()
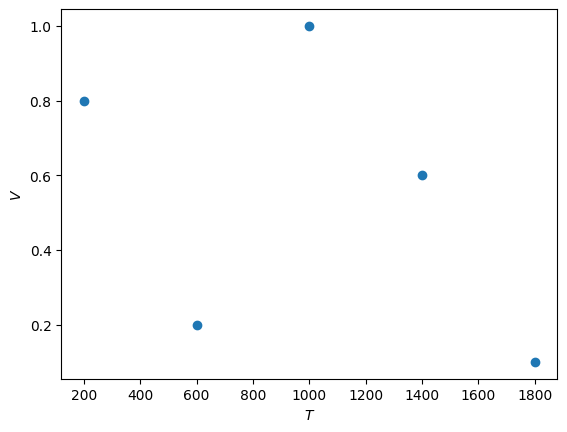
../_images/1d36a4d3a6652ff8826b472f947a2ce3f25c327d4ab3117bc4f01e171abd10b5.png

Finally, \(pV\) against \(T\).

plt.plot(T, p * V, 'o')
plt.xlabel('$T$')
plt.ylabel('$pV$')
plt.show()
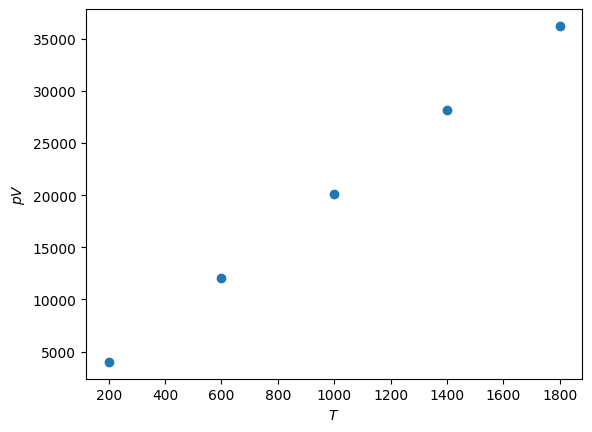
../_images/595f46983aaa8e1a7e2a873c39b4d8a79489e8d1f0804581589f0fa7c44068ea.png

There is a clear linear relationship between \(pV\) and \(T\), the ideal gas relation.

We can now calculate \(n\) for each data point by rearranging the ideal gas law to read,

\[ n = \frac{pV}{RT} \]

and we can use NumPy array to perform this mathematics.

from scipy.constants import R

n = p * V / (R * T)

print(n)

[2.41506889 2.42028069 2.41867706 2.41953615 2.41987978]

We can then find the mean \(n\) and standard error as follows,

mean = np.mean(n)
std_err = np.std(n) / len(n)

print(mean, std_err)

2.4186885144192245 0.0003770883148466002

Note that the len() function will return the number of items in a list as an int.