Simultaneous Equations

The simplest simultaneous equations are two equations with two variables. They are called simultaneous because they must both be solved at the same time, to find a pair of numbers that satisfy both equations. The two equations below form a pair of simultaneous equations:

Note

Similar methods can be applied to 3 equations with 3 unknowns, and more generally n equations with n unknowns.

\[\begin{split} \begin{aligned} 2y - x & = 1 \;\;(1) \\ x + y & = 5 \;\;(2) \end{aligned} \end{split}\]

In order to solve these, we use a method called substitution, shown in the example below. We start by making one of the variables the subject of one of the equations. We then substitute this new expression into the other equation and solve.

Note

In the example here, \(x\) is made the subject of equation \((2)\), but this equally could have been achieved by making \(y\) the subject or equation \((1)\).

Example

Solve the simultaneous equations: \(y + x = 5\;\;(1)\) and \(2y - x = 1\;\;(2)\).

Solution: To solve these, we will make one of the variables the subject. Take equation \((2)\) and make \(x\) the subject:

\[\begin{split} \begin{aligned} 2y = x + 1 \\ 2y - 1 = x \end{aligned} \end{split}\]

As \(x = 2y-1\), we can substitute this expression into \((1)\) to get:

\[\begin{split} \begin{aligned} y + x & = 5 \\ y + (2y - 1) & = 5 \\ 3y - 1 & = 5 \\ 3y & = 6 \\ y & = 2 \end{aligned} \end{split}\]

We have the value of \(y=2\). To find out what \(x\) is we need to substitute \(y=2\) into either one of the equations (both should give the same answer). So if we substitute this into \((1)\), we get:

\[\begin{split} \begin{aligned} y + x & = 5 \\ 2 + x & = 5 \\ x & = 3 \end{aligned} \end{split}\]

We have the solution of \(x=3\) and \(y=2\).

---

The Python sympy library can achieve this.

from sympy import symbols, Eq, solve

x, y = symbols('x y')
eq1 = Eq(y + x, 5)
eq2 = Eq(2 * y - x, 1)
solve([eq1, eq2], [x, y])

{x: 3, y: 2}

---

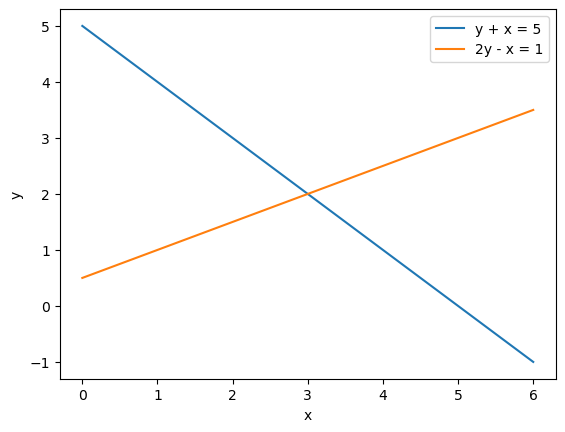
Solving these simultaneous equations can also be done graphically. Below are both equations plotted on the same graph. Notice that the intersection point of the lines is (3, 2), which is what we calculated.

Show code cell source

Hide code cell source

import numpy as np
from sympy import lambdify
import matplotlib.pyplot as plt

f1 = lambdify(x, solve(eq1, y)[0], 'numpy')
f2 = lambdify(x, solve(eq2, y)[0], 'numpy')

x_vals = np.linspace(0, 6, 50)

plt.plot(x_vals, f1(x_vals), label='y + x = 5')
plt.plot(x_vals, f2(x_vals), label='2y - x = 1')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

Example

Stacy’s mother was 30 years old when she was born. At what age is she half her mother’s age?

Solution: To solve this problem, we first need to form equations that describe the information given to us. Let the variables \(s\) and \(m\) denote the age of Stacy and her mother, respectively, then we can write:

• Stacy’s mother is 30 years older than her: \(m = s + 30 \;\;(1)\)

• Stacy’s age is half her mothers: \(s = \frac{1}{2}m\;\;(2)\).

We want to find Stacy’s age \(s\), so to do that, we shall substitute \((1)\) into \((2)\).

• Resulting in: \(s = \frac{1}{2} (s + 30)\)

• Multiply each side by \(2\): \(2s = s+30\)

• Subtract \(s\) from both sides: \(s = 30\)

Stacy will be 30, when she’s half her mother’s age.

---

Similar to the example above, once the equations are formulated, sympy can help.

s, m = symbols('s m')
eq1 = Eq(m, s + 30)
eq2 = Eq(s, 0.5 * m)
solve([eq1, eq2], [m, s])

{m: 60.0000000000000, s: 30.0000000000000}

---

Mass Spectrometry

Results from a mass spectrometry experiment show that 2 fragments of a molecule both contain hydrogen and carbon. The empirical formula for the first fragment is c₂H₅, which as a mass of 29 amu and the second has a formula of C₈H₁₈, with a mass of 114 amu. Calculate the mass of the carbon and hydrogen atoms.

Solution: First, we write the information provided in equations. We shall use the variables \(C\) and \(H\) to be the mass of the carbon and hydrogen, respectively. For the first fragment, we can write \(2C+5H = 29\) and for the second fragment \(8C+18H = 114\). So we have the simultaneous equations:

\[\begin{split} \begin{aligned} 2C+5H & = 29 \;\;\;(1) \\ 8C+18H & = 114 \;\;\;(2) \end{aligned} \end{split}\]

To solve these, we use substitution. In \((1)\), we make \(C\) the subject by first subtracting \(5H\) from both sides to give:

\[ 2C = 29 - 5H \;\;\;(3) \]

From here, we notice that in \((2)\), there is a \(8C\). We can multiply both sides of \((3)\) by 4 to get \(8C = 116 - 20H\), which can be substituted into \((2)\) to give:

\[\begin{split} \begin{aligned} (116 - 20H) + 18H & = 114 \\ 116 - 2H & = 114 \\ 116 - 114 & = 2H \\ 2 & = 2H \\ 1 & = H \end{aligned} \end{split}\]

Now that we have found \(H\), all we need to do is put that value into one of the equations and then we solve for \(C\). Substituted into \((1)\) gives:

\[\begin{split} \begin{aligned} 2C + 5H & = 29 \\ 2C + 5 & = 29 \\ 2C & = 29 - 5 \\ 2C & = 24 \\ C & = 12 \end{aligned} \end{split}\]

---

Naturally, sympy handles this complexity easily.

C, H = symbols('C H')

eq1 = Eq(2 * C + 5 * H, 29)
eq2 = Eq(8 * C + 18 * H, 114)

solve([eq1, eq2], [C, H])

{C: 12, H: 1}

---

Nitrogen Velocity

A molecule of N₂ has a mass of 4.6×10^-26 kg and is at a temperature of 293 K. The nitrogen’s velocity is related to the kinetic energy by the equation:

\[ E_k = \frac{1}{2}mv^2\;\;\;(1) \]

And the kinetic energy is given by:

\[ E_k = \frac{3}{2} k_B T\;\;\;(2) \]

What is the velocity of a nitrogen molecule? (\(k_B = 1.4\times10^{-23}\;\textrm{J K}^{-1}\))

Solution: Considering the variables there are only 2 unknowns, \(E_k\) and \(v\). So we have a pair of simultaneous equations. The first thing is to substitute the expression for \(E_k\) \((2)\) into \((1)\).

\[ \frac{3}{2} k_B T = \frac{1}{2}mv^2 \]

We then re-arrange ths equation to make \(v\) the subject.

• Multiply each side by 2: \(3k_BT = mv^2\)

• Divide by \(m\) on both sides: \(\frac{3k_BT}{m} = v^2\)

• Finally square root: \(\sqrt{\frac{3k_BT}{m}} = v\)

We can now put the numbers in on the left hand side and find that \(v = 520\;\textrm{m s}^{-1}\) (to 2 s.f.).

---

For this example, we can use sympy to evaluate the result.

E_k, m, v, k_B, T = symbols('E_k m v k_B T')

eq1 = Eq(E_k, 0.5 * m * v ** 2)
eq2 = Eq(E_k, 3 / 2 * k_B * T)

result = solve([eq1, eq2], [E_k, v], dict=True)
result

[{E_k: 1.5*T*k_B, v: -1.73205080756888*sqrt(T*k_B/m)},
 {E_k: 1.5*T*k_B, v: 1.73205080756888*sqrt(T*k_B/m)}]

We use the positive result for \(v\).

result[1][v].evalf(subs={m: 4.6e-26, k_B: 1.4e-23, T: 293})

\[\displaystyle 517.225037223098\]

---