Polar Coordinates

With the usual x/y-axis, we will be familiar with coordinates in the form (3,2), meaning that we move 3 units in the x-direction (along the x-axis) and by a move of 2 units in the y-direction. These are Cartesian coordinates.

There is another coordinate system called polar coordinates. These are coordinates in the form (r, θ), where r is the distance to the point from the origin and θ is the angle, in radians, between the positive x-axis and the line form by r. This is all shown in the diagram below.

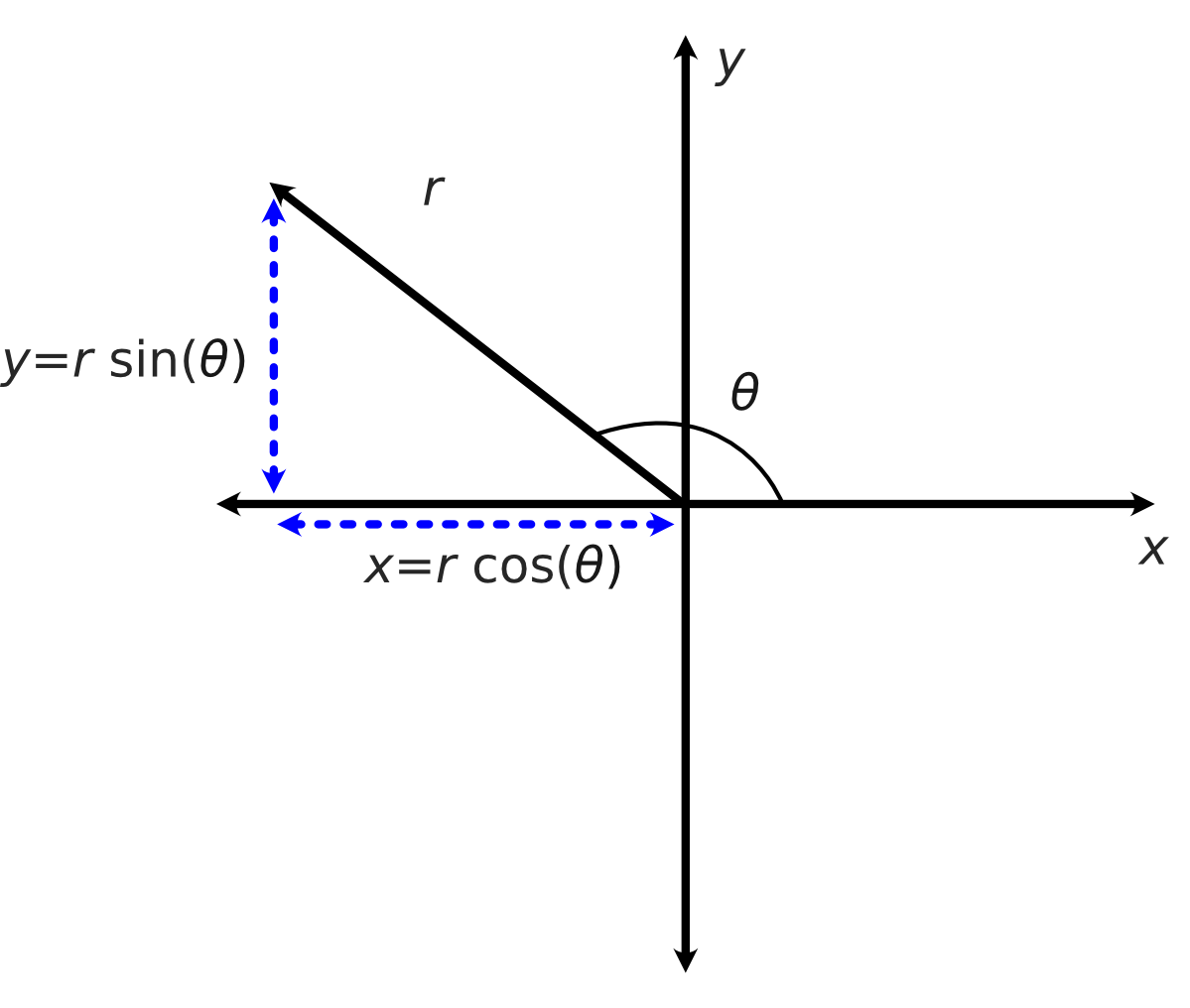
So the point that has Cartesian coordinates (x, y) can also be described in the polar form as (r, θ). From trigonometry and Pythagoras’ Theorem, we have the following relationships:

• \(x = r\cos(\theta)\)

• \(y = r\sin(\theta)\)

• \(r = \sqrt{x^2 + y^2}\)

We can use the formulae above to convert between polar and cartesian coordinates.

Example

A point has polar coordinates \(\left(3, \frac{-\pi}{4}\right)\). What are the corresponding Cartesian coordinates?

Solution: So \(r=3\) and \(\theta = \frac{-\pi}{4}\). So using the formulae above we have:

\[\begin{split} \begin{aligned} x & = r\cos(\theta) = 3 \times \cos\left(\frac{-\pi}{4}\right) = \frac{3\sqrt{2}}{2} \\ y & = r\sin(\theta) = 3 \times \sin\left(\frac{-\pi}{4}\right) = \frac{-3\sqrt{2}}{2} \end{aligned} \end{split}\]

So our Cartesian coordinates are \(\left(\frac{3\sqrt{2}}{2}, \frac{-3\sqrt{2}}{2}\right)\).

---

As we have seen, Python can help with this calculation.

import numpy as np

r = 3
theta = -np.pi / 4

x = r * np.cos(theta)
y = r * np.sin(theta)

x, y

(2.121320343559643, -2.1213203435596424)

---

Example

A point has Cartesian coordiantes \((-2, 3)\). What are the corresponding polar coordinates?

Solution: So we have that \(x=-2\) and \(y=3\). So using the formulae above, we have:

\[ r = \sqrt{x^2 + y^2} = \sqrt{(-2)^2 + 3^2} = \sqrt{13} \]

Now, we can find \(\theta\).

\[ x = r\cos(\theta) \Rightarrow = \cos^{-1}\left(\frac{x}{r}\right) = \cos^{-1}\left(\frac{-2}{\sqrt{13}}\right) = 2.158\ldots \approx 2.16 \;\textrm{rad} \]

So our polar coordinates are \((\sqrt{13}, 2.16)\).

---

Again, with Python.

x = -2
y = 3

r = np.sqrt(x ** 2 + y ** 2)
theta = np.arccos(x / r)

r, theta

(3.605551275463989, 2.1587989303424644)

---