Geometry

Circles: Area, Radius, Diameter, and Circumference

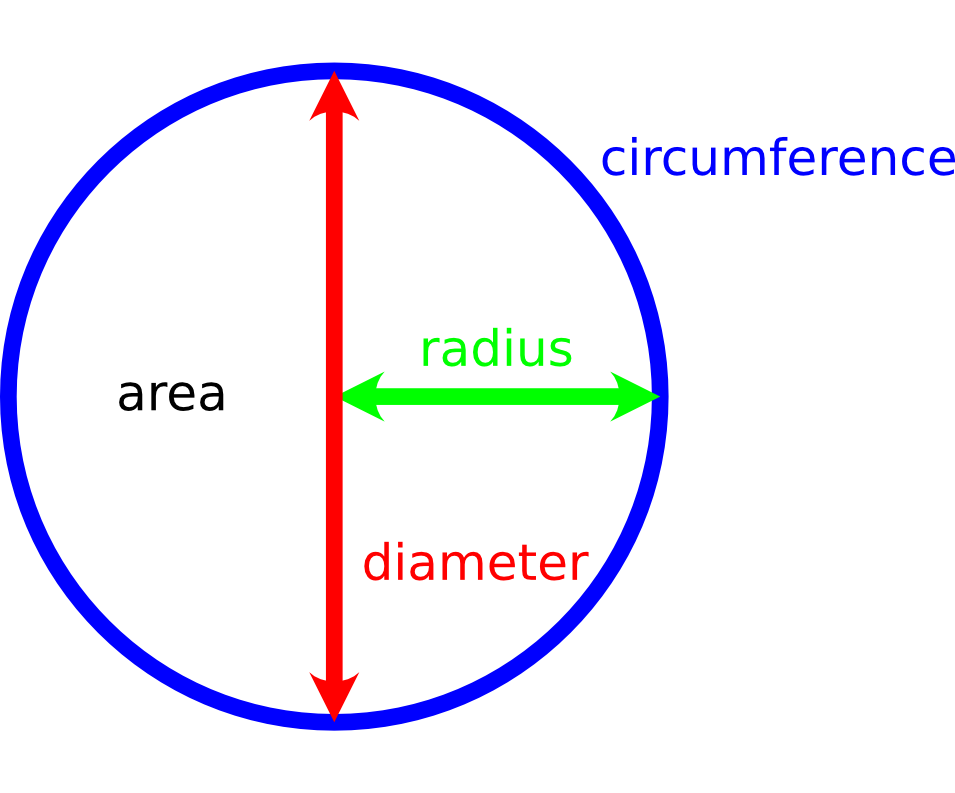
Above, we have a cicle, which shows the area, \(A\), radius, \(r\), diameter, \(d\), and circumference, \(C\), of a circle. These are related by the following equations:

Note

π is the number 3.14159…, which relates the circumference to the diameter \(\pi = \frac{C}{d}\). It has an infinite number of decimal places, that do not repeat.

• \(d=2r\)

• \(A = \pi r^2\)

• \(C = 2\pi r\)

Properties of a Hydrogen Atom

A hydrogen atom has a diameter of 106 pm. For a circle with a diameter of 106 pm, calculate the:

1. Circumference

2. Area

Solution:

1. To find the circumference, first we find the radius

   \[ d = 2r \Rightarrow r=\frac{d}{2} = \frac{106\;\textrm{pm}}{2} = 53\;\textrm{pm}. \]

   Now, we can find the circumference by using:

   \[ C = 2\pi r = 2\pi \times 53\;\textrm{pm} = 333.00\ldots\;\textrm{pm} = 333 \;\textrm{pm} \textrm{ (to 3 s.f.)}. \]

2. As we know \(r = 53\;\textrm{pm}\), we can find the area.

   \[\begin{split} \begin{aligned} A & = \pi r^2 = \pi \times (53\;\textrm{pm})^2 = \pi \times 2.809\ldots\times 10^{-21}\;\textrm{m}^2 \\ & = 8.24\ldots\times 10^{-21}\;\textrm{m}^2 = 8.82\times 10^{-21}\;\textrm{m}^2 \textrm{ (to 2 s.f.)}. \end{aligned} \end{split}\]

---

Python is a natural calculator, so we can compute these values easily.

Python Note

Here, we import π as an object, pi. There stores the value of π to machine precision.

from pint import UnitRegistry
from numpy import pi 

ureg = UnitRegistry()

d = 106 * ureg.pm

r = d / 2
C = 2 * pi * r
C

333.0088212805181 picometer

A = pi * r ** 2
A.to(ureg.m ** 2)

8.824733763933728×10^-21 meter²

---

Spheres: Volume and Surface Area

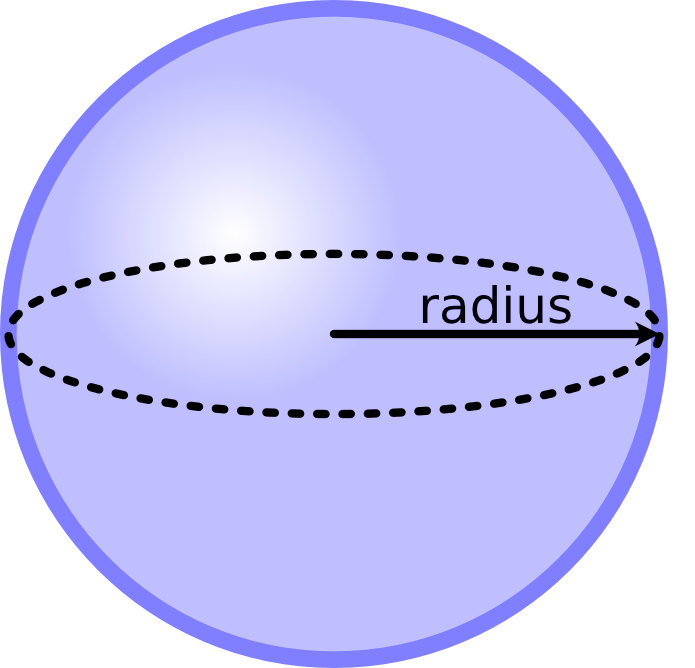
Above, we have a picture that shows the radius of a sphere, which is the distance from the centre to the surface. The volume, \(V\) of a sphere is given by:

\[ V = \frac{4\pi r^3}{3} \]

and the surface area, \(A_S\), is given by:

\[ A = 4\pi r^2 \]

Flourine Sphere

A flourine atom is measured to have a radius of 60 pm. For a sphere with a radius of 60 pm, calculate the:

1. Volume

2. Surface area

Solution:

1. As \(r= 60\;\textrm{pm}\), we can find the volume by using the formula:

   \[\begin{split} \begin{aligned} V & = \frac{4\pi r^3}{3} = \frac{4\pi \times (60\;\textrm{pm})^3}{3} \\ & = \frac{4 \pi \times 2.16 \times 10^{-31}\;\textrm{m}^3}{3} \\ & = 9.05\times10^{-31}\;\textrm{m}^3\textrm{ (to 3 s.f.)}. \end{aligned} \end{split}\]

2. We can find the surface area by using the formula:

   \[\begin{split} A_S = 4 \pi r^2 = 4\pi \times (60\;\textrm{pm})^2 \\ & = 4\pi \times 3.6 \times 10^{-21}\;\textrm{m}^2 \\ & = 4.52\times 10^{-20}\;\textrm{m}^2\textrm{ (to 3 s.f.)}. \end{split}\]

---

Again, using Python.

r = 60 * ureg.pm

V = (4 * pi * r ** 3) / 3
V.to(ureg.m ** 3)

9.047786842338604×10^-31 meter³

A = 4 * pi * r ** 2
A.to(ureg.m ** 2)

4.5238934211693014×10^-20 meter²

---