Introduction to Differentiation

Note

Remember that the gradient is a measure of how steep the graph is at a certain point.

Recall the equation of a straight line is of the form of \(y = mx+c\), where \(m\) is the gradient and \(c\) is the intercept. We can find the gradient \(m\) of a straight line using the triangle method with the formula, \(m=\frac{\Delta y}{\Delta x}\).

As the gradient of a straight line is the same at every point on the line, it is easy to find. With a curve, this is not the case. Consider the graph \(y = 5e^{-x}\) shown below, we will use the triangle method with two different triangles, and show we get two different values for the gradient.

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-0.2, 5.5, 100)
y = 5 * np.exp(-x)

plt.plot(x, y, label='f(x) = 5 * exp(-x)')
plt.axvline(x=0, color='gray', linestyle='-')
plt.axhline(y=0, color='gray', linestyle='-')
plt.axvline(x=1, color='red', linestyle='--', ymin=0.11, ymax=0.38)
plt.axvline(x=2, color='red', linestyle='--', ymin=0.11, ymax=0.23)
plt.axvline(x=2, color='red', linestyle='-', ymin=0.23, ymax=0.38)
plt.axhline(y=0.68, color='red', linestyle='--', xmin=0.125, xmax=0.44)
plt.axhline(y=1.85, color='red', linestyle='--', xmin=0.125, xmax=0.3)
plt.axhline(y=1.85, color='red', linestyle='-', xmin=0.3, xmax=0.44)
plt.text(-0.3, 0.68, '$y_1$', fontsize=12, ha='center', va='center')
plt.text(-0.3, 1.86, '$y_2$', fontsize=12, ha='center', va='center')
plt.text(1, -0.5, '$x_1$', fontsize=12, ha='center')
plt.text(2, -0.5, '$x_2$', fontsize=12, ha='center')
plt.text(1.5, 2.25, '$\Delta x$', fontsize=12, ha='center', va='center')
plt.text(2.25, 1.265, '$\Delta y$', fontsize=12, ha='center', va='center')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-1, None)
plt.ylim(-1, None)
plt.legend()
plt.show()

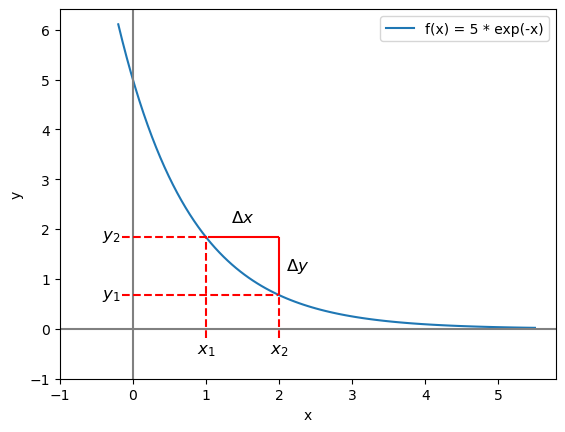
Using the triangle method with the triangle in the graph above gives:

\[ \textrm{gradient} = \frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{y_2-y_1}{x_2-x_1} = \frac{0.68 - 1.85}{2-1} = -1.17 \]

---

Python functions can help with this computation.

def f(x):
    return 5 * np.exp(-x)

x_1 = 1
x_2 = 2

gradient = (f(x_2) - f(x_1)) / (x_2 - x_1)
gradient

-1.162720789674148

---

Now if we use the triangle method again by this time with a larger triangle as in the graph below:

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-0.2, 5.5, 100)
y = 5 * np.exp(-x)

plt.plot(x, y, label='f(x) = 5 * exp(-x)')
plt.axvline(x=0, color='gray', linestyle='-')
plt.axhline(y=0, color='gray', linestyle='-')
plt.axvline(x=1, color='red', linestyle='--', ymin=0.11, ymax=0.38)
plt.axvline(x=3, color='red', linestyle='--', ymin=0.11, ymax=0.17)
plt.axvline(x=3, color='red', linestyle='-', ymin=0.17, ymax=0.38)
plt.axhline(y=0.25, color='red', linestyle='--', xmin=0.125, xmax=0.59)
plt.axhline(y=1.85, color='red', linestyle='--', xmin=0.125, xmax=0.3)
plt.axhline(y=1.85, color='red', linestyle='-', xmin=0.3, xmax=0.59)
plt.text(-0.3, 0.68, '$y_1$', fontsize=12, ha='center', va='center')
plt.text(-0.3, 1.86, '$y_2$', fontsize=12, ha='center', va='center')
plt.text(1, -0.5, '$x_1$', fontsize=12, ha='center')
plt.text(3, -0.5, '$x_2$', fontsize=12, ha='center')
plt.text(2, 2.2, '$\Delta x$', fontsize=12, ha='center', va='center')
plt.text(3.2, 1.05, '$\Delta y$', fontsize=12, ha='center', va='center')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(-1, None)
plt.ylim(-1, None)
plt.legend()
plt.show()

\[ \textrm{gradient} = \frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{y_2-y_1}{x_2-x_1} = \frac{0.25 - 1.85}{3-1} = -1.17 \]

---

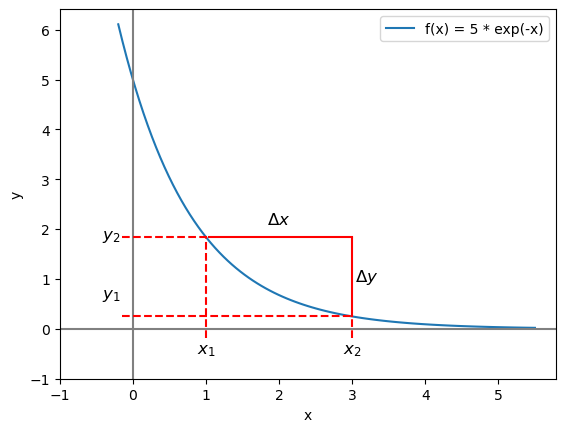
x_2 = 3

gradient = (f(x_2) - f(x_1)) / (x_2 - x_1)
gradient

-0.795230932008946

We have two different values for the gradient of the curve. This is because the value of the gradient is not the same at all points on the curve, unlike a straight line. This should be obvious as we can see that the steepness of the graph changes along the curve. This means it is quite hard to find the gradient of a curve using the triangle method, and so we need a new method.

Differentiation allows us to find the gradient of a graph. The reason that this works is because when we differentiate, we are calculating how one variable changes due to a change in another (in other words, the rate of change). This is useful in chemistry: for example, we might wish to know how the concentration of the reactant [OH^-], changes with time t.

Notation

When we use the triangle method, we are finding \(\frac{\Delta y}{\Delta x}\), where \(\Delta\) means the difference. Similarly, when we differentiate, we are effectively drawing an infinitely small triangle to calculate the rate of change (or gradient). This might seem quite an abstract concept and a full explanation lies beyond the scope of this webpage, where we present the main properties of differentiation. When differentitating, we use the notation:

\[ \frac{dy}{dx} \]

Note

We don’t use \(\Delta\) anymore, as this represents a larger, not infinitely small, difference. You may see a lower case delta, \(\delta\), used instead of \(d\) in some sources.

where the \(d\) stands for an infinitely small difference.

Example

The derivative of \(x^2\), as you will soon learn, is \(2x\). Using the notation above, we would write this as:

\[ \textrm{If }y=x^2\textrm{, then }\frac{dy}{dx} = 2x \]

Recall how we can write either \(y\) or \(f(x)\), this leads to another notation for differentiation, displayed in the table below:

Note

We may sometimes refer to \(\frac{d}{dx}\) as the differential operator.

Function	Derivative	Pronounciation
\(y\)	\(\frac{dy}{dx}\)	d-y by d-x or d-y d-x
$f(x)4	\(f'(x)\)	f prime of x or f dash of x
\(f(x)\)	\(\frac{d}{dx}[f(x)]\)	d by d-x of f of x

Example

So if \(f(x)=x^2\) then we can write the deriviative in the following ways:

\[ f'(x) = 2x \]

OR $\( \frac{d}{dx}(x^2) = 2x \)$

Important

When we find \(\frac{dy}{dx}\), we said we are differentiating \(y\) with respect to \(x\). Now suppose instead that we have the equation \(\theta = t^2\) then:

\[ \frac{d\theta}{dt} = 2t \]

This works in the same way as we have seen for \(x\) and \(y\), but in this case we have it in terms of \(\theta\) and \(t\) and would say we are differentiating \(\theta\) with respect to \(t\).