Trigonometry

Angles

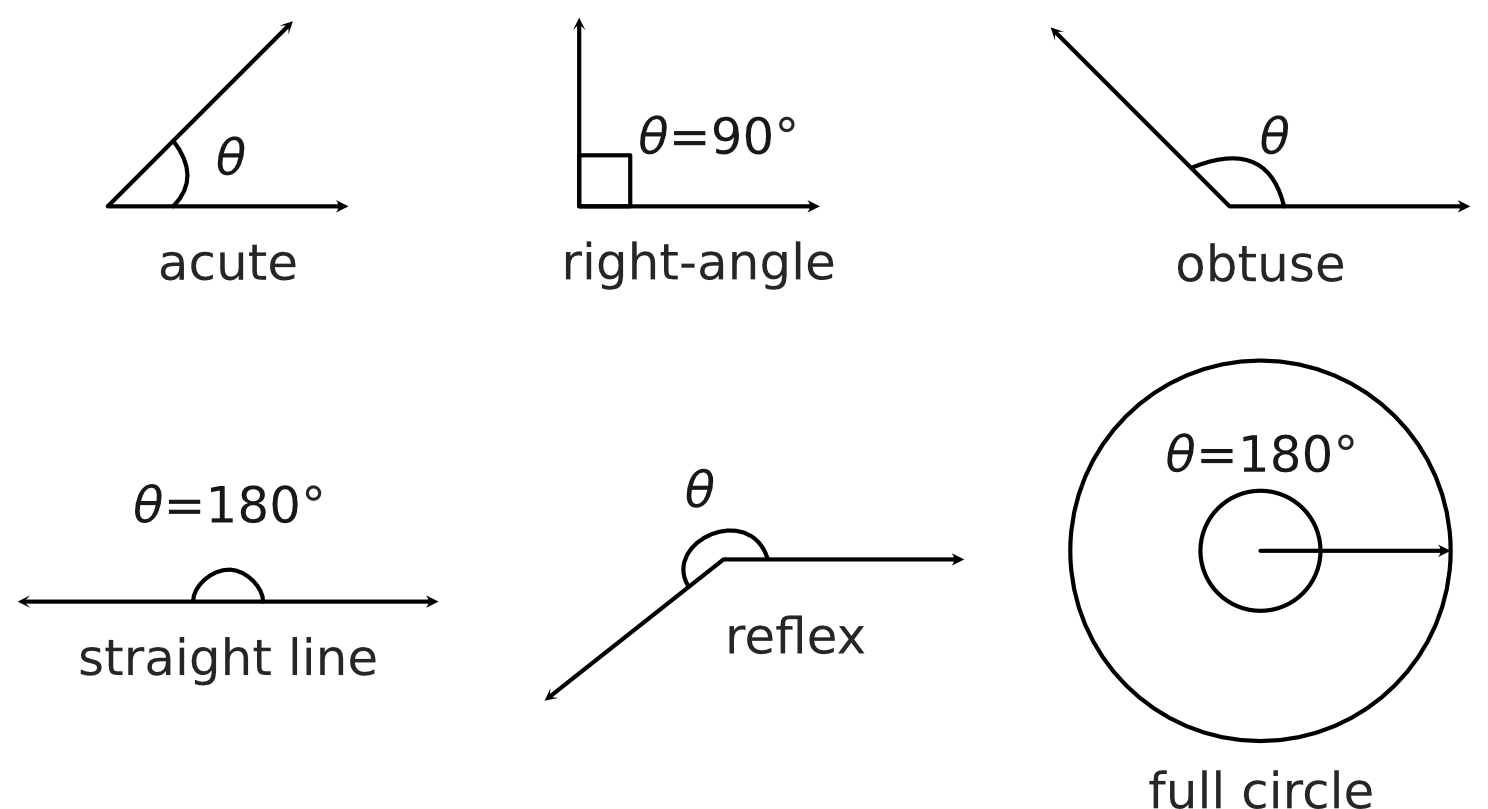
Angle Type	Size of Angle
Acute Angle	\(0^\circ < \theta < 90^\circ\)
Right Angle	\(\theta = 90^\circ\)
Obtuse Angle	\(90^\circ < \theta < 180^\circ\)
Straight Line	\(\theta = 180^\circ\)
Reflex Angle	\(180^\circ < \theta < 360^\circ\)
Full Circle	\(\theta < 360^\circ\)

Radians

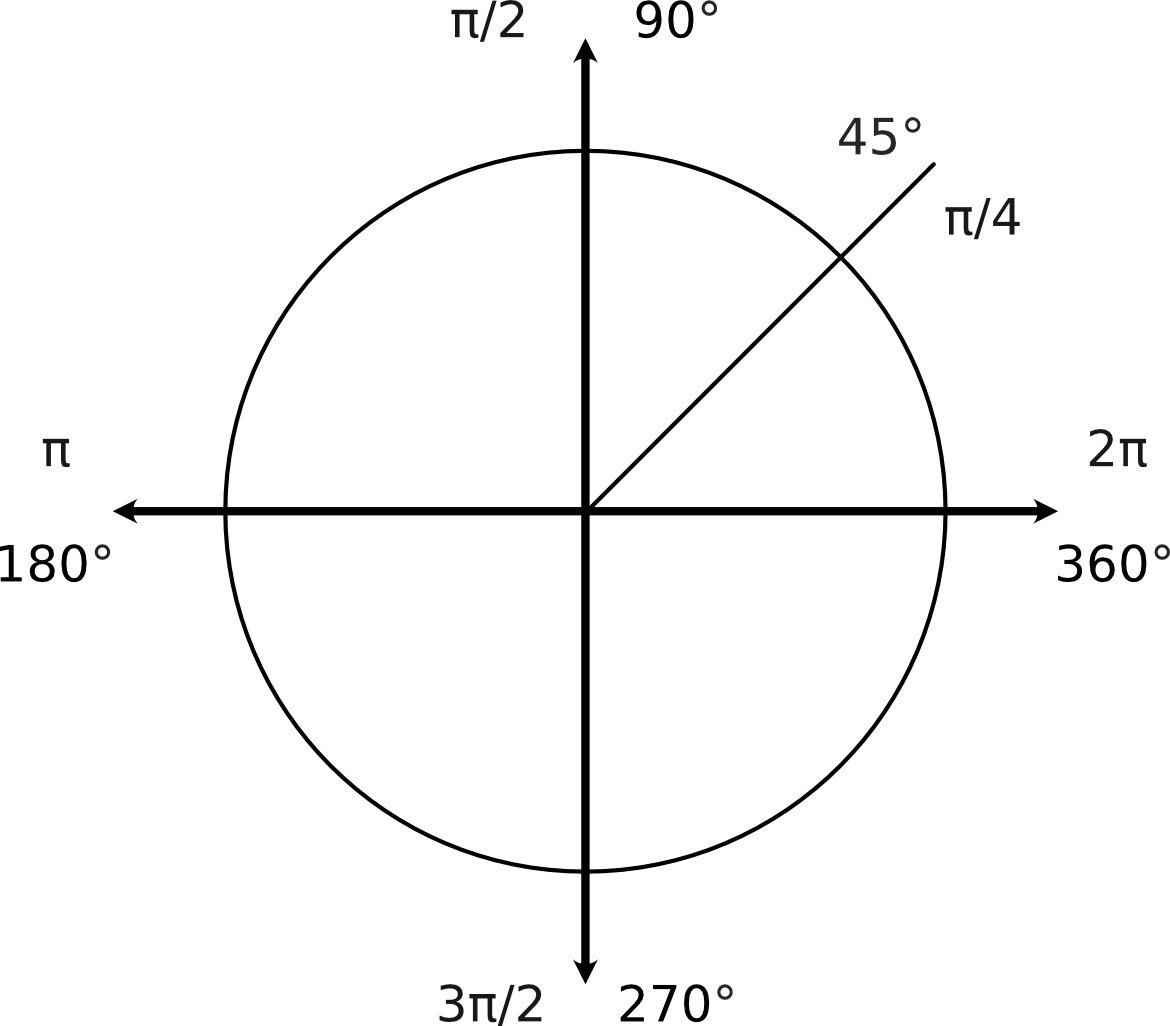
We often use degrees to measure angles, however, we have another measurement of angles called radians. Instead of splitting the full circle into 360°, it is split into 2π radians. We must use radians in calculus (differentiation and integration), complex numbers and polar coordinates. This may seem new and complicated at first, however, it is no different to thinking that we could measure length in miles or metres.

Below, we have a full circle, showing some angles in degrees and what they are in radians.

We may wish to convert between degree and radians. In order to turn \(x^\circ\) degrees into radians, we use the formula:

\[ x = \frac{x^\circ}{360^\circ} \times 2\pi \]

In order to convert \(x\) radians into degrees, we use rearrange the formula:

\[ x^\circ = \frac{x}{2\pi} \times 360^\circ \]

Example

Convert the following:

1. \(60^\circ\) into radians.

2. \(\frac{3\pi}{8}\) radians to degrees.

Solution:

1. \(\frac{x^\circ}{360^\circ} \times 2\pi = \frac{60^\circ}{360^\circ} \times 2\pi = \frac{\pi}{3}\;\textrm{rad}\)

2. \(\frac{x}{2\pi} \times 360^\circ = \frac{\left(\frac{3\pi}{8}\right)}{2\pi} \times 360^\circ = \frac{3}{16} \times 360^\circ = 67.5^\circ\)

---

The pint library has the ability to perform this unit conversion.

from numpy import pi
from pint import UnitRegistry

ureg = UnitRegistry()

(60 * ureg.degree).to(ureg.radian)

1.0471975511965976 radian

(3 * pi / 8 * ureg.radian).to(ureg.degree)

67.5 degree

---

Right-Angle Triangles

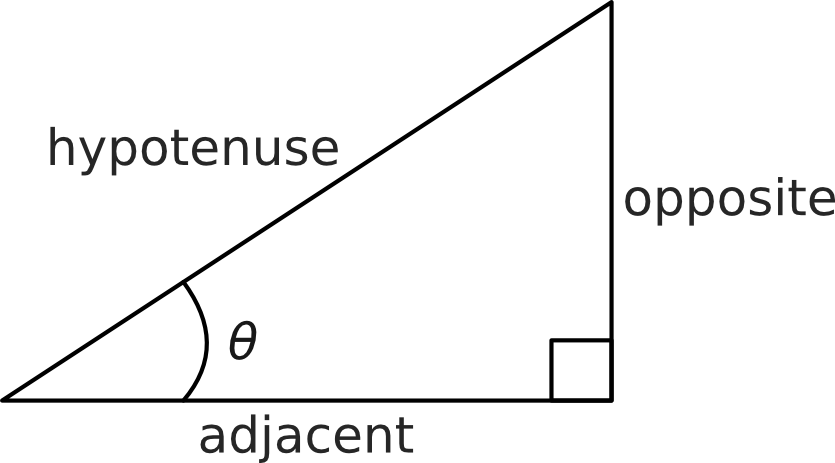
As shown in the diagram above, when given a right-angled triangle with one of the non-right angles labelled &\theta;, then we label the sides as follows:

• The longest side is called the hypotenuse, this is always the side opposite the right angle.

• The side that is opposite the angle θ is called the opposite. The side that is next to the angle θ is call the adjacent.

Pythagoras’ Theorem

Pythagoras’ theroem relates only to right-angled triangles. So given a right-angled triangle, such as the one below, it states:

\[ a^2 + b^2 = c^2 \]

where \(c\) is the length of the hypotheuse and \(a\) and \(b\) are the lengths of the other two sides of the triangle.

Example

Find the length of \(x\) and \(y\) in the following triangles

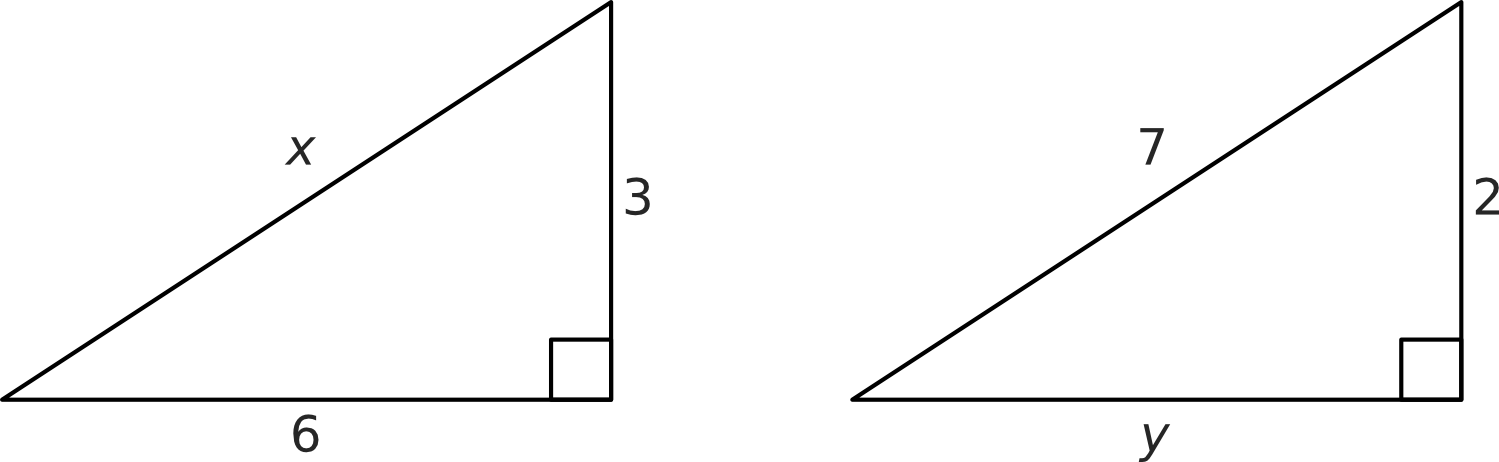
Solution:

1. Using Pythagoras’ Theorem we know that, since \(x\) is the hypotenuse,

\[ x^2 = 3^2 + 6^2 \Rightarrow x = \sqrt{45} \approx 6.708 \]

2. Using Pythagoras’ Theorem we know that,

\[ 7^2 = y^2 + 2^2 \Rightarrow y = \sqrt{45} \approx 6.708 \]

Crystalline Distances

Below is the structure of solid sodium chloride (sodium in blue, chloride in black). If the distance between the centres of adjacent chlroide and sodium ions is 278 pm, what is the next shortest distance between such ions? i.e., what is the length of the red dashed line?

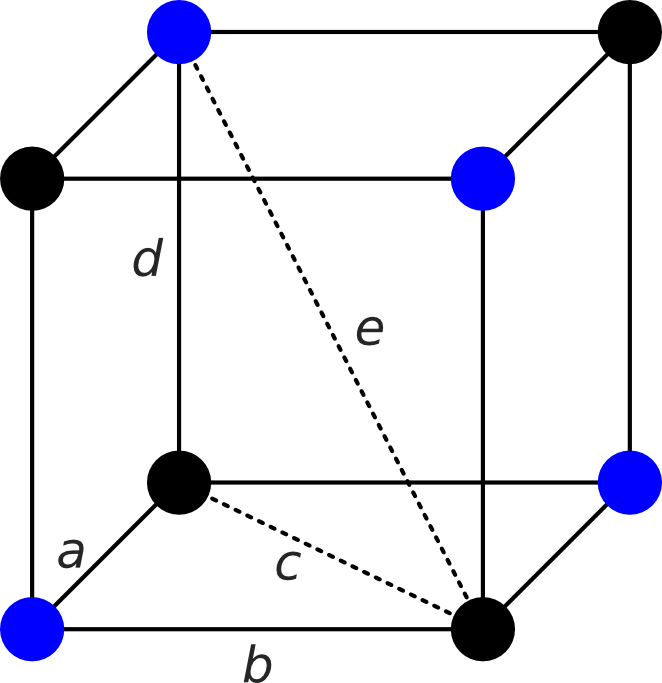
Solution: First we consider the triangle from the cube lattice above, with lengths \(a\), \(b\), and \(c\). This is a right-angled triangle, shown below on the left, so we can apply Pythagoras’ Theorem.

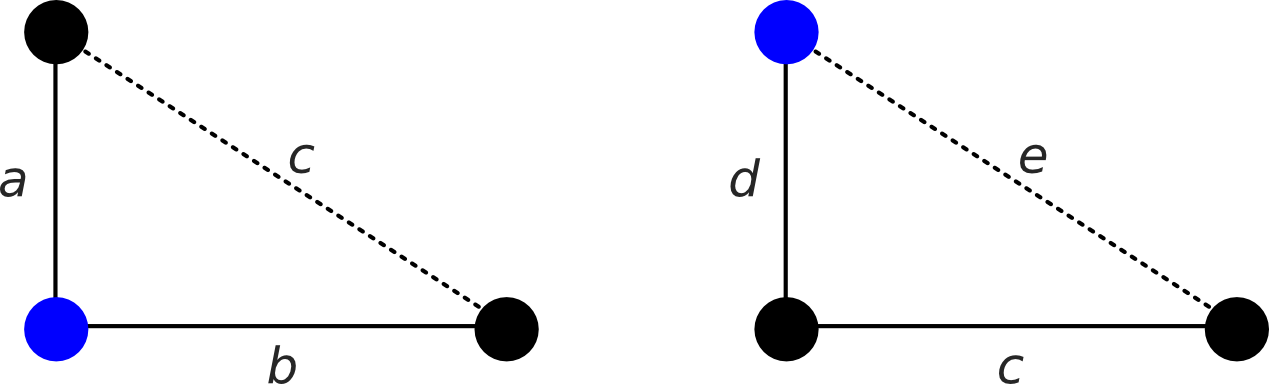
We know from the question tht the distance between adjacent chloride and sodium ions is 278 pm, so \(a = b = 278\;\textrm{pm}\). So we have, using Pythagoras’ Theorem,

\[ c^2 = 278^2 + 278^2 \Rightarrow c = 393\;\textrm{pm} \]

Now, consider the triangle from the cube lattice with lengths \(c\), \(d\), \(e\). This is a right-angled triangle, shown above on the right, so we can again apply Pythagoras’ Theorem.

We know from the question that the distance between adjacent chloride and sodium ions is 278 pm, so \(d=278\;\textrm{pm}\) and from our previous calculations, we know \(c=393\;\textrm{pm}\). So we have, using Pythagoras Theorem,

\[ e^2 = 278^2 + 393^2 \Rightarrow e = 481\;\textrm{pm}. \]

SOHCAHTOA

Given our right-angled triangle, we start by defining sine, cosine, and tangent, before reviewing what their graphs look like.

Note

The angle θ is measured in radians in the following graphs on the x-axis.

Sine Function

We define sine as the ratio of the opposite to the hypotenuse.

\[ \sin(\theta) = \frac{\textrm{Opposite}}{\textrm{Hypotenuse}} \]

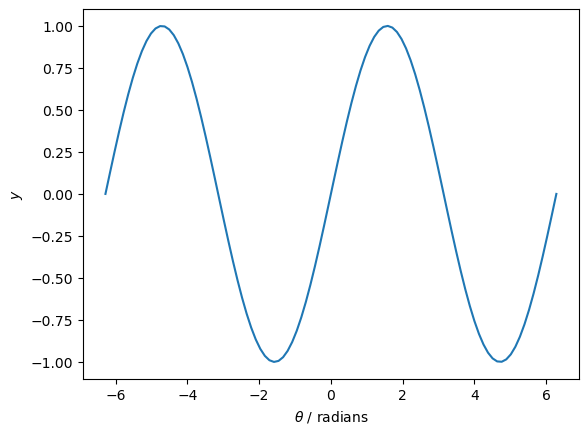
Part of the graph of \(y=\sin(\theta)\) is shown below.

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

x = np.linspace(-2 * np.pi, 2 * np.pi, 100)
y = np.sin(x)

ax.plot(x, y)
ax.set_xlabel(r'$\theta$ / radians')
ax.set_ylabel(r'$y$')
plt.show()

Cosine Function

We define cosine as the ratio of the adjacent to the hypotenuse.

\[ \cos(\theta) = \frac{\textrm{Adjacent}}{\textrm{Hypotenuse}} \]

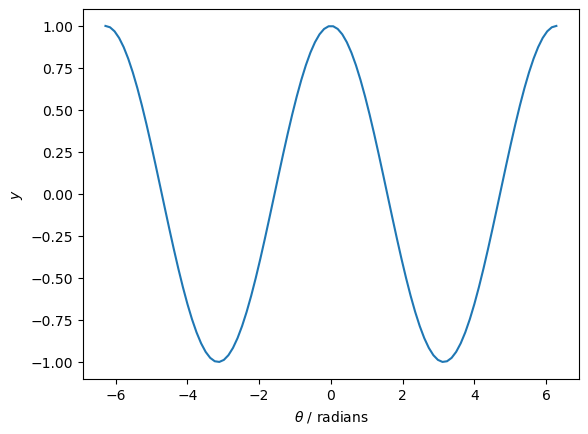
Part of the graph of \(y=\cos(\theta)\) is shown below.

Show code cell source

Hide code cell source

fig, ax = plt.subplots()

x = np.linspace(-2 * np.pi, 2 * np.pi, 100)
y = np.cos(x)

ax.plot(x, y)
ax.set_xlabel(r'$\theta$ / radians')
ax.set_ylabel(r'$y$')
plt.show()

Tangent Function

We define tangent as the ratio of the opposite to the adjacent.

\[ \tan(\theta) = \frac{\textrm{Opposite}}{\textrm{Adjacent}} \]

This leads to the relationship \(\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}\) shown below:

\[\begin{split} \begin{aligned} \tan{\theta} & = \frac{\textrm{Opposite}}{\textrm{Adjacent}} = \frac{\textrm{Opposite}\times\textrm{Hypotenuse}}{\textrm{Adjacent}\times\textrm{Hypotenuse}} \\ & = \frac{\frac{\textrm{Opposite}}{\textrm{Hypotenuse}}}{\frac{\textrm{Adjacent}}{\textrm{Hypotenuse}}} = \frac{\sin{\theta}}{\cos{\theta}} \end{aligned} \end{split}\]

The graph of \(y=\tan(\theta)\) is shown below.

Show code cell source

Hide code cell source

fig, ax = plt.subplots()

x = np.linspace(-3 / 2 * np.pi, 3 / 2 * np.pi, 100)
y = np.tan(x)

ax.plot(x, y)
ax.set_xlabel(r'$\theta$ / radians')
ax.set_ylabel(r'$y$')
ax.set_ylim(-5, 5)
plt.show()

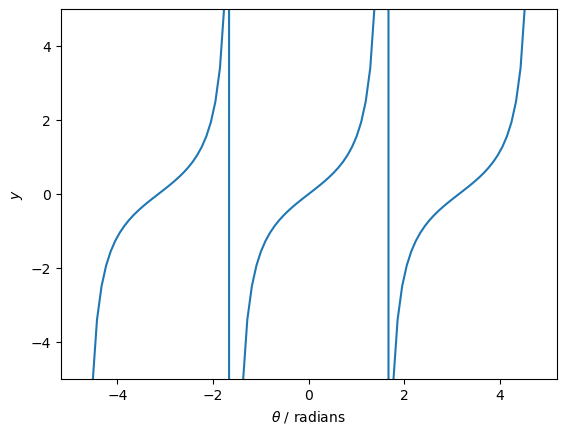
The definition of sine, cosine, and tangent are often more easily remembered as SOHCAHTOA. We can use the formulas in SOHCAHTOA to calculate the size of angles and the lengths of sides in right-angled triangles.

Note

Beaware, some of these questions use degrees and other radians.

Example

Using SOHCAHTOA, find the lengths of \(x\), \(y\), and \(z\), in the right-angled triangles below.

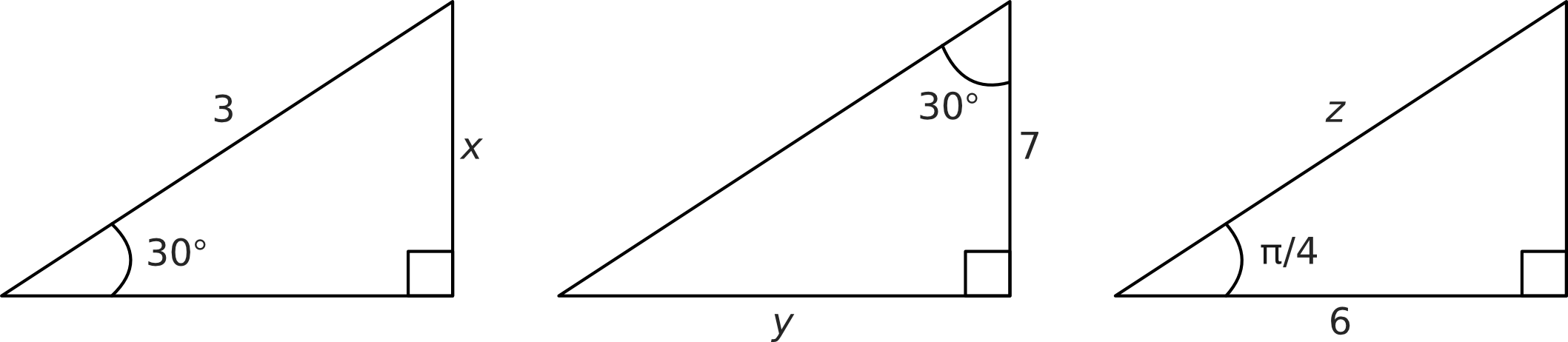
Solution: For shorthand, we have used \(\textrm{H}\) to denote hypotenuse, \(\textrm{O}\) the opposite, and \(\textrm{A}\) the adjacent.

1. We know the length of the hypotenuse and wish to find the opposite, hence we need to use:

   \[ \sin(\theta) = \frac{\textrm{O}}{\textrm{H}} \Rightarrow \sin(30^\circ) = \frac{\textrm{O}}{3} \Rightarrow \textrm{O} = \sin(30^\circ) \times 3 = \frac{3}{2} \]

2. We know the length of the adjacent and wish to find the opposite, hence we need to use:

   \[ \tan(\theta) = \frac{\textrm{O}}{\textrm{A}} \Rightarrow \tan(30^\circ) = \frac{\textrm{O}}{7} \Rightarrow \tan(30^\circ)\times 7 = \frac{7\sqrt{3}}{3} \]

3. We know the length of the adjacent are wish to find the hypotenuse, hence we need to use:

   \[ \cos(\theta) = \frac{\mathrm{A}}{\mathrm{H}} \Rightarrow \cos\left(\frac{\pi}{4}\right) = \frac{6}{\textrm{H}} \Rightarrow \textrm{H} = \frac{6}{\cos\left(\frac{\pi}{4}\right)} = 6\sqrt{2} \]

---

We can use Python to help us with these computations.

Python Note

The NumPy trigonometric functions assume that the inputs are in radians. So for the computations with degrees, we use the np.radians function to convert.

np.sin(np.radians(30)) * 3

1.4999999999999998

np.tan(np.radians(30)) * 7

4.04145188432738

6 / np.cos(np.pi / 4)

8.48528137423857

---

Carbon-Carbon Bond

A carbon-carbon bond has a length of 154 pm. If the bond is positioned at an angle of 30° to a surface, as shown below. What is the projected length of the bond?

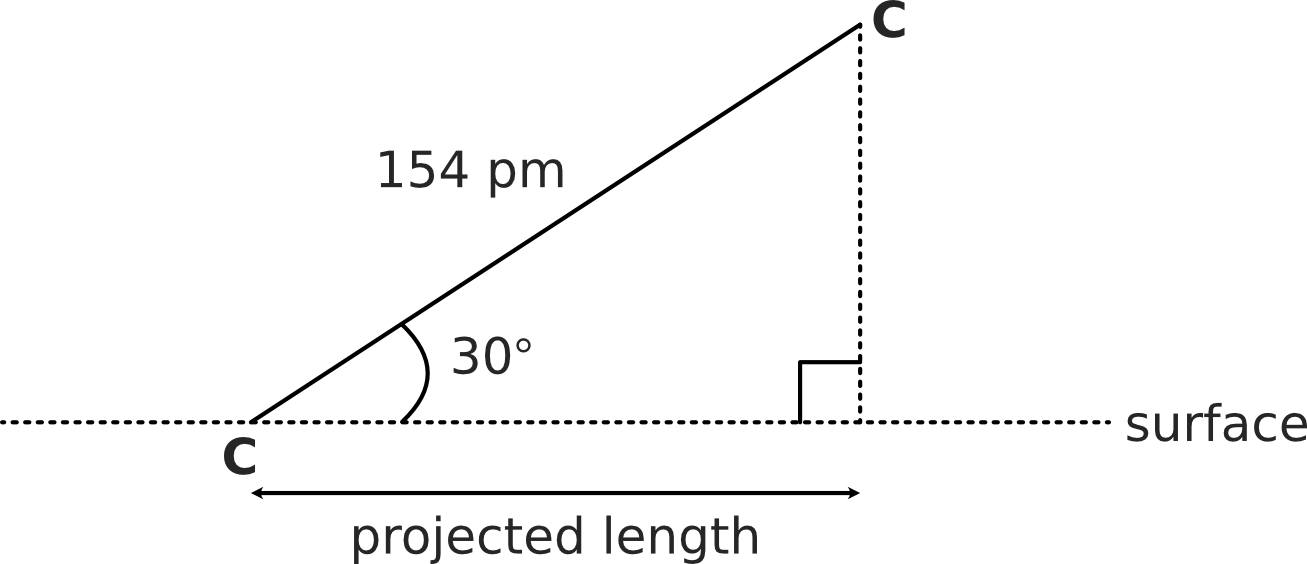
Solution: To solve this, we should first note that we have a right-angled triangle and can therefore use SOHCAHTOA. We know the hypotenuse, which is 154 pm and want to find the projected length, which is the adjacent. So, we need to use:

\[ \cos(\theta) = \frac{\textrm{A}}{\textrm{H}} \Rightarrow \cos(30^\circ) = \frac{\textrm{A}}{154\;\textrm{pm}} \Rightarrow A = \cos(30^\circ) \times 154\;\textrm{pm} = 77\sqrt{3}\;\textrm{pm} \approx 133\;\textrm{pm} \]

---

With Python

np.cos(np.radians(30)) * 154 * ureg.pm

133.36791218280356 picometer

---

Inverse Function and Rearranging Trigonometric Functions

We may be given the lengths of two sides of a right-angled triangle and be asked to find the angle, θ, between them or be ased to rearrange an equation with a trigonometric function. In order to do these, we need to introduce the inverse trigonometric function:

• The inverse function of sine is sin^-1(θ), can also be denoted as arcsin(θ).

• The inverse function of cosine is cos^-1(θ), can also be denoted as arccos(θ).

• The inverse function of tangent is tan^-1(θ), can also be denoted as arctan(θ).

We use the inverse trigonometric functions with SOHCAHTOA to find the values of anlges in right-angled triangles in which two of the lengths of the sides have been given. We do this as followis, suppose we know that:

\[ \sin(\theta) = \frac{1}{2} \]

To find θ, we can apply the inverse sine function to both sides of the equation,

\[\begin{split} \begin{aligned} \sin^{-1}\left(\sin(\theta)\right) & = \sin^{-1}\left(\frac{1}{2}\right) \\ \theta & = \sin^{-1}\left(\frac{1}{2}\right) \\ \theta & = 30^\circ \end{aligned} \end{split}\]

---

We can use a calculator, or Python, to find \(\sin^{-1}\left(\frac{1}{2}\right) = 30^\circ = \frac{\pi}{6} \;\textrm{radians}\).

Python Note

NumPy uses arc* for the inverse functions. Also, note the use of np.degrees, to convert the radians result to degrees.

np.degrees(np.arcsin(1/2)), np.arcsin(1/2)

(30.000000000000004, 0.5235987755982989)

---

Example

Using SOHCAHTOA find the size of the angles \(B\), \(C\), and \(D\), in the right-angled triangles below.

Solution:

1. We know the length of the hypotenuse and the opposite.

   \[ \sin(\theta) = \frac{\textrm{O}}{\textrm{H}} \Rightarrow \sin(B) = \frac{3}{5} \Rightarrow \sin^{-1}\left(\frac{3}{5}\right) = 36.9^\circ/0.64\;\textrm{rad} \]

2. We know the length of the adjacent and the opposite.

   \[ \tan(\theta) = \frac{\textrm{O}}{\textrm{A}} \Rightarrow \tan(C) = \frac{6}{5} \Rightarrow \tan^{-1}\left(\frac{6}{5}\right) = 50.2^\circ/0.88\;\textrm{rad} \]

3. We know the length of the hypotenuse and the adjacent.

   \[ \cos(\theta) = \frac{\textrm{A}}{\textrm{H}} \Rightarrow \cos(D) = \frac{6}{11} \Rightarrow \cos^{-1}\left(\frac{6}{11}\right) = 56.9^\circ/0.99\;\textrm{rad} \]

---

Once again, using the arc* NumPy functions.

np.arcsin(3/5), np.degrees(np.arcsin(3/5))

(0.6435011087932844, 36.86989764584402)

np.arctan(6/5), np.degrees(np.arctan(6/5))

(0.8760580505981934, 50.19442890773481)

np.arccos(6/11), np.degrees(np.arccos(6/11))

(0.9938649815584398, 56.944268849146)

---

Note

When squaring trigonometric functions, such as \(\left(\sin(x)\right)^2\), \(\left(\cos(x)\right)^2\), and \(\left(\tan(x)\right)^2\), we use the notation \(\sin^2(x)\), \(\cos^2(x)\), and \(\tan^2(x)\) are used in the same way. This is also true more generally, for example \(\left(\sin(x)\right)^n\) is denoted \(\sin^n(x)\).

Bond Angles

The position of certain bands in the infra-red spectrum of SO₂ can be used to determine the angle θ of the O-S-O bonds. The analysis leads to the equation:

\[ \sin^2{\left(\frac{\theta}{2}\right)} = 0.769 \]

Find the value of \(\theta\) in degrees.

Solution: First, we can square root both sides to remove the square on the sin function. This gives us:

\[\begin{split} \begin{aligned} \sqrt{\sin^2\left(\frac{\theta}{2}\right)} & = \sqrt{0.769} \\ \sin{\left(\frac{\theta}{2}\right)} & = 0.8769\ldots \end{aligned} \end{split}\]

We now take the inverse of both sides:

\[\begin{split} \begin{aligned} \sin^{-1}\left(\sin\left(\frac{\theta}{2}\right)\right) & = \sin^{-1}(0.8769) \\ \frac{\theta}{2} & = \sin^{-1}(0.8769) \\ \frac{\theta}{2} & = 61.27\ldots \\ \theta & = 123^\circ \textrm{ (to 3 s.f.)} \end{aligned} \end{split}\]

---

We can check this with Python.

np.degrees(np.arcsin(np.sqrt(0.769)) * 2)

122.54759369030917

---