Equations and Functions

Equations and Functions#

Physical and chemical quantities are often linked in equations.

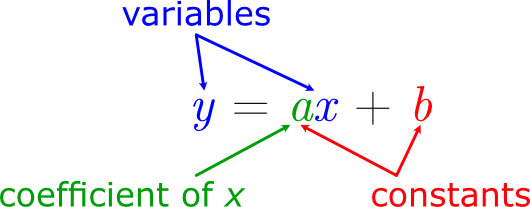
The function y=ax+b, with the variables (y and x), constants (a nd b) and coefficient of x (a) identified.

  • Variables are quantities that can take different values; they can vary.

  • Constants are fixed numbers, so unlike variables cannot change.

  • The coefficient of \(x\) is the constant before the \(x\). In the same way for the equation \(y=8t^2+t\), the coefficient of \(t^2\) is \(8\) and the coefficient of \(t\) is \(1\).

What is a Function?#

Relationships between quantities are reffered to as functions, which we usually denote \(f(x)\), pronouned “f of x”.

In general, we have \(y\) is a function of \(x\):

\[ y = f(x) \]

This means that \(y\) is equal to an expression made up of \(x\)’s. For example, \(y=x+3\) or \(y=e^{3x}\).

  • So a function takes a quantity (a variable or number) and applied operations to it. This produces a new quantity.

  • Although we have used the notation \(f(x)\), there is no reason why we could not use \(g(x)\) or even \(\phi(x)\).

  • We can also have \(f(x)\) or \(f(\theta)\) if we have functions made up of variables other than \(x\). For example, \(f(z) = z^2\) or \(g(\theta) = \cos{(\theta)}\).

Example

The function \(f\) takes a variable, doubles it and then subtracts 2. The function \(g\) halves its input. What is:

  1. \(f(3)\)?

  2. \(f(x)\)?

  3. \(g(8)\)?

Solution:

  1. The function \(f\) takes the input and doubles it then subtracts 2. With the input being 3, we can find \(f(3)\) by applying those steps to the number 3. When we double it, we get 6. Subtract 2 then gives us 4. So our final answer it \(f(3)=4\).

  2. We do these same steps but with the variable \(x\) instead of a number. First we double it to give \(2x\). Then we subtract 2 to give \(2x-2\). We now have that \(f(x) = 2x-2\).

  3. We apply the function \(g\) to 8. Halving 8 will give us 4, hence \(g(8)=4\).

Using Python, we can write code functions to implement out mathematical functions.

def f(x):
    """
    Doubles x and subtracts 2.
    
    :param x: The input number.
    :return: The result of the operation.
    """
    return 2 * x - 2

def g(x):
    """
    Halves x.
    
    :param x: The input number.
    :return: The result of the operation.
    """
    return x / 2

f(3)

4

g(8)

4.0

Gas Pressure

In an experiment, the pressure of a gas is monitored as the temperature is changed, while the volume and amount of gas remain constant and the following relationship was established:

\[ p = 0.034 T \]

  1. Identiy the variables and coefficients in the equation.

  2. What is \(p\) a function of?

  3. Given that the temperature is 343 K, what is the value of \(p\)?

Solution:

  1. In the experiment, \(p\) can vary and \(T\) can also vary. This means that \(p\) and \(T\) are both variables. The 0.034 is multiplying the \(T\), making it a coefficient. The coefficient of \(p\) is 1.

  2. In the equation, \(p=0.034T\), the only other variable apart from \(p\) is \(T\). Hence \(p\) is a function of \(T\) and \(T\) alone.

  3. To find this, we will substitute 343 for \(T\) into the equation to get, \(p=0.034 \times 343 = 11.662 = 11.7 (\textrm{to 3 s.f.})\).

As above, we can create a Python function for the pressure at a given temperature, T.

def pressure(T):
    """
    Calculates the pressure based on temperature.
    
    :param T: The temperature in Kelvin.
    :return: The pressure in Pascals.
    """
    return 0.034 * T

pressure(343)

11.662

Functions with Multiple Variables#

Functions can also be of multiple variables. The function:

\[ y = f(x,z) \]

means that the function \(f\) takes in a value of \(x\) and also a value of \(z\) to give an output so \(x\) and \(z\) are both variables. For example:

\[ y = f(x,z) = xz + 2x + 2 \]

This function would input variables \(x\) and \(z\) and give their product plus \(2x\) plus \(2\) as an output. If \(x=2\) and \(z=\frac{1}{2}\), then \(y=7\).

Ideal Gas Law

Consider the ideal gas equation:

\[ pV = nRT \]

The temperature \(T\) can be expressed as a function of the pressure, \(p\), and the volume, \(V\), which are variables. This can be written as:

\[ T = f(p, V) = \frac{pV}{nR} \]

Python code functions can have more than one variable. Therefore, we could create an ideal gas law function.

from scipy.constants import R

n = 2

def ideal_gas_law(p, V):
    """
    Calculates the ideal gas law.
    
    :param P: Pressure in Pascals.
    :param V: Volume in cubic meters.

    :return: Temperature in Kelvin.
    """
    return p * V / (n * R)
Contents