Operations with Vectors

Operations with Vectors#

Scalar Multiplication#

Scalar multiplicaiton is when we multiply a vector by a scalar. We do this by multiplying each component of the vector by the scalar. This can be expressed as:

\[ \lambda \times (x, y, z) = (\lambda x, \lambda y, \lambda z) \]

where, \(\lambda\) is a real number.

Example

Simplify \(7(-12, 4)\).

Solution: We multiply each component of the vector by 7 giving:

\[ (7 \times -12, 7 \times 4) = (-84, 28) \]

This can be performed with a NumPy array.

import numpy as np

7 * np.array([-12, 4])

array([-84,  28])

Vector Addition and Subtraction#

When we add or subtract two vectors, we add or subtract each of the individual components of the vectors. This can be expressed as:

\[ (a, b, c) + (x, y, z) + (a+x, b+y, c+z) \]

where \((a, b, c)\) and \((x, y, z)\) share the same base vectors.

Important

If the vectors have a different number of base components, for example \((3, 6) + (1, 0, 7)\) we cannot complete the addition. For all vector on vector operations, both vectors must have the same number of base components.

Example

  1. \((2, 2, 0) + (5, -1, 3)\)

  2. \(3(a, 4a, 0) - a(7, 0, -1)\)

  3. \((1, 3, 8) + (2, 1, -5) + (-1, 2, -1)\)

Solution:

  1. \((2, 2, 0) + (5, -1, 3) = (3+5, 2-1, 0+3) = (7, 1, 3)\)

  2. \(3(a, 4a, 0) - a(7, 0, -1) = (3a, 12a, 0)-(7a, 0, -a) = (3a-7a, 12a-0, 0+a)\) \( = (-4a, 12a, a)\)

  3. \((1, 3, 8)+(2, 1, -5) + (-1, 2, -1) = (1+2-1, 3+1+2, 8-5-1) = (2, 6, 2)\)

Again, NumPy can implement this for numerical examples.

np.array([2, 2, 0]) + np.array([5, -1, 3])

array([7, 1, 3])

np.array([1, 3, 8]) + np.array([2, 1, -5]) + np.array([-1, 2, -1])

array([2, 6, 2])

However, the middle example includes the algebraic \(a\), which is possible to compute with pure NumPy. Instead sympy should be used.

from sympy import symbols

a = symbols('a')

3 * np.array([a, 4 * a, 0]) - a * np.array([7, 0, -1])

array([-4*a, 12*a, a], dtype=object)

Vector Mulitplication: Dot Product#

There are two ways of multiplying two vectors together. The first is the dot (or scalar) product, which is defined to be:

\[ \vec{A}\cdot\vec{B} = |\vec{A}||\vec{B}| \cos(\theta) \]

where \(\theta\) is the angle between \(\vec{A}\) and \(\vec{B}\).

Important

Taking the dot product of two vectors produces a scalar quantity.

Given two vectors, the dot product can also be calculated in the following way:

\[\begin{split} \begin{pmatrix} a \\ b \\ c \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} = ax + by + cz \end{split}\]

The dot product can be thought of as how much one vector is pointing in the direction of the other. This is indicated with the plot below.

Hide code cell source

 
import matplotlib.pyplot as plt
from matplotlib.patches import Arc

A = np.array([3, 2])
B = np.array([4, 0])
Adash = np.array([3, -0.2])

fig, ax = plt.subplots()

ax.quiver(0, 0, A[0], A[1], angles='xy', scale_units='xy', scale=1, color='b')
ax.text(A[0]/2, A[1]/2, r'$\vec{A}$', ha='right', va='bottom', color='b')
ax.quiver(0, 0, B[0], B[1], angles='xy', scale_units='xy', scale=1, color='r')
ax.text(B[0]/2, B[1]/2+0.05, r'$\vec{B}$', ha='right', va='bottom', color='r')
ax.quiver(0, -0.2, Adash[0], 0, angles='xy', scale_units='xy', scale=1, color='b')
ax.text(Adash[0]/2, -0.25, r'$\vec{A}\cos(\theta)$', ha='right', va='top', color='b')
arc = Arc([0, 0], 2, 2, theta1=0, theta2=33.69, color='r')
ax.add_patch(arc)
ax.text(0.8, 0.27, r'$\theta$', va='center', ha='center', color='r')

ax.set_aspect('equal')
ax.set_xlim(-0.5, 4.5)
ax.set_ylim(-0.5, 2.5)

plt.show()
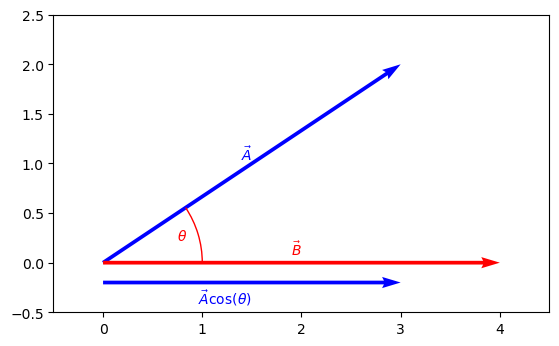
../_images/f1b3b2e828d1519c850ab2c3527a3daa5dd9745fc307857d565c0a229c597e2f.png

The part of \(\vec{A}\) that goes in the same direction as \(\vec{B}\) has a length of \(|\vec{A}|\cos{(\theta)}\), making the dot product the length of \(\vec{B}\) times the length of \(\vec{A}\) that is in the same direction as \(\vec{B}\).

Example

Calculate the following:

  1. \(\begin{pmatrix} 3 \\ 9 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -2 \\ 10 \end{pmatrix}\)

  2. \(\begin{pmatrix} 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} \sqrt{2} \\ \sqrt{2} \end{pmatrix}\)

Solution:

  1. \(\begin{pmatrix} 3 \\ 9 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -2 \\ 10 \end{pmatrix} = 3 \times 1 + 9 \times (-2) + 1 \times 10 = 3 - 18 + 10 = -5\)

  2. \(\begin{pmatrix} 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} \sqrt{2} \\ \sqrt{2} \end{pmatrix} = 1\times \sqrt{2} + 0 \times\sqrt{2} = \sqrt{2}\)

The NumPy library includes a np.dot function that can be used to find the dot product of two vectors.

np.dot(np.array([3, 9, 1]), np.array([1, -2, 10]))

-5

np.dot(np.array([1, 0]), np.array([np.sqrt(2), np.sqrt(2)]))

1.4142135623730951

Angle Between Force Vectors

An ion moving through solution has 2 forces acting upon it, a resistive force from the medium with a vector of \((3, \sqrt{7}, 3)\), and an electromagnetic foce from an electric field with a vector of \((-5, 3, 4)\). What is the angle between these two vectors?

Solution: To calculate this, we find the dot product of the two vectors and then employ the definition of the dot product to find the angle. The dot product of the two vectors is:

\[\begin{split} \begin{pmatrix} 3 \\ \sqrt{7} \\ 3 \end{pmatrix} \cdot = 3 \times (-5) + \sqrt{7} \times 3 + 3 \times 4 = -3 + 3\sqrt{7} \approx 4.937 \end{split}\]

Using the definition \(\vec{A}\cdot\vec{B} = |\vec{A}||\vec{B}| \cos{(\theta)}\), we can not find out what \(\theta\) is. First, we must find the magnitudes of the two vectors:

\[ |(3, \sqrt{7}, 3)| = \sqrt{3^2 + 7 + 3^2} = \sqrt{25} = 5 \]

and

\[ |(-5, 3, 4)| = \sqrt{(-5)^2 + 3^2 + 4^2} = \sqrt{50} = 5\sqrt{2} \]

Putting all this information into the equation \(\vec{A}\cdot\vec{B} = |\vec{A}||\vec{B}| \cos{(\theta)}\), gives us:

\[\begin{split} \begin{aligned} 3 (\sqrt{7} - 1) & = 5 \times 5\sqrt{2}\cos(\theta) \\ \frac{3 (\sqrt{7} - 1)}{5 \times 5\sqrt{2}} & = \cos(\theta) \\ \theta = \cos^{-1}(0.1396\ldots) & = 81.97^\circ\ldots = 82.0^\circ \textrm{ to 3 s.f.} \end{aligned} \end{split}\]

As one would expect, we can bring aspects of NumPy together to perform this with code.

A = np.array([3, np.sqrt(7), 3])
B = np.array([-5, 3, 4])

angle = np.arccos(np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B)))
np.rad2deg(angle)

81.97260125982753

Work/Force

What is the work done \(w\) be the vector force \(\vec{F} = (3t\vec{i} + 3\vec{j})\;\textrm{N}\) on a particle of velocity \(\vec{V} = (5\vec{i} - t\vec{j})\;\textrm{ms}^{-1}\) in the time interval \(0 < t < 3\;\textrm{s}\), given that:

\[ w = \int_0^3 \vec{F}\cdot\vec{v} \textrm{d}t \]

Solution: First, we must find the dot product \(\vec{F}\cdot\vec{v}\).

\[ \vec{F}\cdot\vec{v} = (3t\vec{i} + 3\vec{j}) \cdot (5\vec{i} - t\vec{j}) = 3t\times 5 + 3 \times (-t) = 12t \]

Now we have found the dot product, we can substitute it in the integral and solve.

\[\begin{split} \begin{aligned} w & = \int_0^3 \vec{F}\cdot\vec{v} \textrm{d}t \\ & = \int_0^3 = 12t \textrm{d}t \\ & = \big[6t^2\big]_0^3 \\ & = \big[6\times 3^2\big] - \big[6 \times 0^2\big] = 54\;\textrm{J} \end{aligned} \end{split}\]

Let’s look at how we can get a numerical estimate of this result with the rectangle rule approach to estimate the integral. We start with defining a range of t, from 0 to 3.

width = 0.0001
t = np.arange(0, 3, width)
t += width / 2
t

array([5.00000e-05, 1.50000e-04, 2.50000e-04, ..., 2.99975e+00,
       2.99985e+00, 2.99995e+00])

Next, we compute the vector \(\vec{F}\) for all the values of \(t\).

F = np.array([3 * t, 3 * np.ones_like(t)])
F

array([[1.50000e-04, 4.50000e-04, 7.50000e-04, ..., 8.99925e+00,
        8.99955e+00, 8.99985e+00],
       [3.00000e+00, 3.00000e+00, 3.00000e+00, ..., 3.00000e+00,
        3.00000e+00, 3.00000e+00]])

The same is done for \(\vec{v}\).

v = np.array([5 * np.ones_like(t), -t])

And we can perform the dot product.

dot_product = np.sum(F * v, axis=0)

Finally, we estimate the integral using the rectangle rule.

np.sum(dot_product * width)

54.00000000000001

This is a good estimate of the value found algebraically above.

Vector Multiplication: Cross Product#

The cross product (or vector product) is defined to be:

\[ \vec{A}\times \vec{B} = |\vec{A}||\vec{B}| \sin{(\theta)}\vec{\hat{n}} \]

where, \(\theta\) is the angle between the two vectors and \(\vec{\hat{n}}\) is the unit vector in the direction of the new vector.

Important

The cross product takes two vectors and produces a new vector. This new vector is in the direction **perpendicular** to the plane that \(\vec{A}\) and \(\vec{B}\) are in. It is only possible to take the cross product of two 3-D vectors (and technically 7-D vectors as well).

The cross product is also dependent on the order that the vectors appear in the product. If we change the order of the vectors in a cross product, then our answer becomes negative. The vector points in the opposite direction.

\[ \vec{A}\times\vec{B} = -\vec{B}\times\vec{A} \]

The right hand rule determines the way which the vector produced will point. We use the rule as follows:

Curl your fingers from the first vector in the cross product to the second vector and the direction your thumb points is the direction of the vector produced by the cross product.

Hide code cell source

 
A = np.array([-4, -4])
B = np.array([0, -5])

fig, ax = plt.subplots()

ax.quiver(0, 0, A[0], A[1], angles='xy', scale_units='xy', scale=1, color='g')
ax.text(A[0]/2, A[1]/2, r'$\vec{A}$', ha='right', va='bottom', color='g')
ax.quiver(0, 0, B[0], B[1], angles='xy', scale_units='xy', scale=1, color='b')
ax.text(B[0]/2 - 0.1, B[1]/2, r'$\vec{B}$', ha='right', va='bottom', color='b')
arc = Arc([0, 0], 2, 2, theta1=270-45, theta2=270, color='r')
ax.add_patch(arc)
ax.text(-0.5, -1.1, r'$\theta$', va='center', ha='center', color='r')

ax.set_aspect('equal')
ax.set_xlim(-5, 0.5)
ax.set_ylim(-6, 0.5)

plt.show()
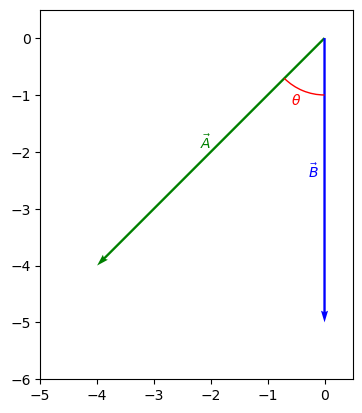
../_images/933f0eead0cfd02487a6b248aa6b662d488659581e5b4d541820efc828c56186.png

In this case, \(\vec{A} \times \vec{B}\) will point out of the page, and \(\vec{B}\times\vec{A}\) will point into the page.

Calculating the Cross Product#

When using the standard base vector of \(\vec{\hat{i}}\), \(\vec{\hat{j}}\), and \(\vec{\hat{k}}\), we can calculate the cross product by considering the cross product of the base vectors with each other.

\[\begin{split} \begin{aligned} \vec{i}\times\vec{i} = \vec{j}\times\vec{j} = \vec{k}\times\vec{k} & = \vec{0} \\ \vec{i}\times\vec{j} = -\vec{j}\times\vec{i} & = \vec{k} \\ \vec{j}\times\vec{k} = -\vec{k}\times\vec{j} & = \vec{i} \\ \vec{k}\times\vec{i} = -\vec{i}\times\vec{k} & = \vec{j} \end{aligned} \end{split}\]

Taking the cross products of two vectors is just like expanding brackets. The cross product of two general vectors \((a\vec{i} + b\vec{j} + c\vec{k}) \times (x\vec{i} + y\vec{j} + z\vec{k})\), would give \(ax(\vec{\vec{i}\times\vec{i}}) + ay(\vec{i}\times\vec{j}) + az(\vec{i}\times\vec{k})+\ldots\). Fully expanded and simplified gives:

\[ (a\vec{i} + b\vec{j} + c\vec{k}) \times (x\vec{i} + y\vec{j} + z\vec{k}) = (bz-cy)\vec{i} + (cx-az)\vec{j} + (ay-bx)\vec{k} \]

where, \(a\), \(b\), \(c\), \(x\), \(y\), and \(z\) are real numbers.

Example

Calculate the following cross product:

\[\begin{split} \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} \times \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \end{split}\]

*Solution: So to find this, we use the formula above, where \(a=3\), \(b=1\), \(c=-2\), \(x=2\), \(y=-1\), \(z=1\), and therefore:

\[\begin{split} \begin{aligned} & (bz-cy)\vec{i} + (cx-az)\vec{j} + (ay-bx)\vec{k} \\ = & \left(1\times 1 - (-2) \times (-1)\right)\vec{i} + \left((-2) \times 2 - 3 \times 1\right)\vec{j} + \left(3\times (-1) - 1 \times 2\right)\vec{k} \\ = & -1\vec{i} - 7\vec{j} - 5\vec{k} \end{aligned} \end{split}\]

This could also be written:

\[\begin{split} \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} \times \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ -7 \\ -5 \end{pmatrix} \end{split}\]

The NumPy library can also be used to compute the cross product between two arrays.

np.cross(np.array([3, 1, -2]), np.array([2, -1, 1]))

array([-1, -7, -5])
Contents