Solving Quadratic Equations

Solving Quadratic Equations#

Solving a quadratic equation involves finding all possible values of \(x\) that satify \(ax^2 + bx + c = 0\). The values of \(x\) that satify this equation are called the roots.

Not that when \(a=0\), the quadratic equation reduces to a simple linear equation \(bx+c=0\), which is easy to solve. Also when \(a\neq 0\), we can divide through by \(a\) to get an equivalent equation of the form \(x^2+bx+c=0\).

There are three methods that can be used to solve a quadratic:

  1. Completing the square

  2. Inspection

  3. The quadratic formula

Completing the Square#

When a quadratic is in the form \(x^2 + 2bx + b^2\), it is known as a perfect square, because it can be faactorised into a squared linear term \((x+b)^2\). However, when a quadratic is not a perfect square, we have the relationship below:

\[ x^2 + 2bx + c = (x+b)^2 + (c-b^2) \]

Hence, if we are trying to solve \(x^2 + 2bx + c = 0\), then we can rewrite this as \((x+b)^2 + (c-b^2) = 0\) and then rearrange to find \(x\).

Example

Find the value of \(x\) that make \(x^2 + 4x - 1 = 0\).

Solution: We can see that \(2b = 4\) and \(c=-1\), so from the equation above, we can change the quadratic into the form with a perfect square:

\[\begin{split} \begin{aligned} x^2 + 4x - 1 & = 0 \\ (x+2)^2 + (-1 - (2^2)) & = 0 \\ (x+2)^2 - 5 & = 0 \end{aligned} \end{split}\]

We can now rearrange and take the square root of both sides:

\[\begin{split} \begin{aligned} (x+2)^2 & = 5 \\ x + 2 & = \pm\sqrt{5} \\ x & = -2 \pm\sqrt{5} \end{aligned} \end{split}\]

When we take the square root of both sides in this previous example, we need to remember that both \((-\sqrt{5})^2\) and \((+\sqrt{5})^2\) are equal to 5; the expression \(\pm\sqrt{5}\) indicates that both sides are included. The two different roots for this equation are shown on the graph below.

Hide code cell source

 
import numpy as np 
import matplotlib.pyplot as plt

x = np.linspace(-5, 1, 1000)

fig, ax = plt.subplots()

ax.plot(x, x ** 2 + 4 * x - 1)
ax.axhline(0, color='k', ls='--')
ax.set_xlabel('$x$')
ax.set_ylabel(r'$x^2 + 4x - 1$')
plt.show()
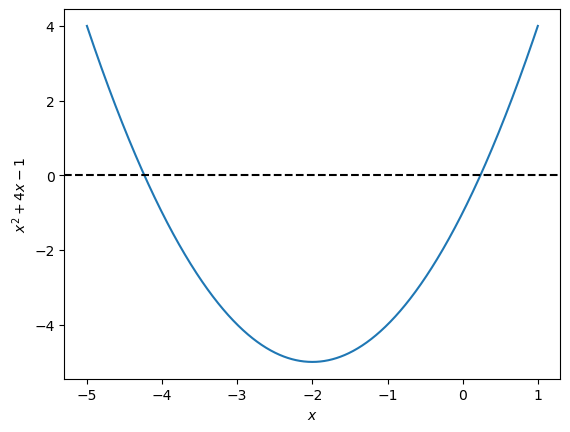
../_images/205574bc3d61e820bf78e3a02d413a64a18b56247c0582818840ba78ba7171df.png

The dashed horizontal line is where \(y=0\), so the points where the curve crosses this line are the roots (where \(x^2 + 4x - 1 = 0\)). The graph goes through a point just ot the left of \(x=-4\) and just to the right of \(x=0\). These correspond to \(x = -2-\sqrt{5}\) and \(x = -2 + \sqrt{5}\), respectively.

The sympy.solve function is capable of finding these roots.

from sympy import symbols, solve

x = symbols('x')
solve(x**2 + 4*x - 1, x)

[-2 + sqrt(5), -sqrt(5) - 2]

Solving by Inspection#

If we have a quadratic with integer coefficients, it is sometimes possible to solve it by inspection. So if the quadratic \(x^2+bx+c\) can be factorised to give \((x+A)(x+B)\), we have the roots of the equation are \(-A\) and \(-B\). We have the following rules for solving by inspection:

  • \(c\) will be the product of \(A\) and \(B\)

  • \(b\) will be the sum of \(A\) and \(B\)

In other words, if we are trying to solve \(x^2+bx+c = 0\), then we need to find two numbers \(A\) and \(B\) such that their sum is \(b\) and product is \(c\). We can then write the equation as \((x+A)(x+B)= 0\) and our roots will be \(x=-A\) and \(x=-B\).

Example

Find \(x\) by inspection in the following \(x^2 + 5x = 0=6\).

Solution: Since we want to factorise this, we need to find two numbers that add to 5 and multiply to 6. The best way to do this is to think about what the factors of 6 are. We have 1 and 6, as well as 2 and 3. We can instantly see that \(2+3=5\), so these are the numbers required. We can rewrite the original equation

\[ x^2+5x+6 = (x+2)(x+3) = 0 \]

Now that we have the quadratic factorised, we can find out what \(x\) is. We notice if either of the terms in the brackets is 0, then the whole thing will be 0. This gives two situations:

\[ x + 2 = 0 \;\;\;\textrm{OR}\;\;\; x+3 = 0 \]

When we find out what \(x\) is for each of those, we see that the roots are \(-2\) and \(-3\). These are both solutions to this quadratic equation.

sympy can double check our inspection.

solve(x**2 + 5 * x + 6, x)

[-3, -2]

Inspection with Negative Coefficients#

Inspection is easy when all the coefficieints are positive, but when they are negative you need to consider a few things. First if \(c\) is negative then one of \(A\) or \(B\) will be negative. This is because when a negative number multiples a positive numebr the result will be negative. Secondly, you would look at \(b\), if it is positive, then the larger number of \(A\) and \(B\) is positive and vice versa.

Take the example \(x^2-4x -5\). We first look at what factors 5 has: here the only factors are 1 and 5. Then we notice that since \(c\) is negative, one of \(A\) or \(B\) is negative and one is positive. Finally, since \(b=-4\) is negative, the sum \(A+B\) is negative and this forces us to chose \(A=-5\) and \(B=1\), giving us \(x^2-4x -5 = (x-5)(x+1)\).

Example

Factorise the following:

  1. \(x^2+4x-12\)

  2. \(x^2-6x-40\)

Solution:

  1. From the signs, we can deduce that one of \(A\) or \(B\) is negative and, since \(b=4\), \(A+B=4\), i.e., is positive. The factors of 12 are 1 and 12, 2 and 6, and 3 and 4. The pair of number that we need are therefore \(A=6\) and \(B=-2\), giving us \(x^2+4x-12 = (x+6)(x-2)\).

  2. The signs tell us that one of \(A\) or \(B\) is negative and, since \(b=-6\), \(A+B=-6\), i.e., is negative. Looking at the factors of 40, we can see that -10 and 4 would produce the requires result (\(-10 + 4 = -6\)), giving us \(x^2 - 6x - 40 = (x-10)(x+4)\).

Finally, if \(c\) is positive by \(b\) is negative, both \(A\) and \(B\) would be negative, since they would give a positive product by a negative sum.

Example

Factorise \(x^2-8x+15\).

Solution: Since \(c=15\) is positive, we know that both \(A\) and \(B\) have the same sing and, since \(b=-8\), \(A+B=-8\), we see that they must both be negative. Looking at the factors of 15, we can see that -5 and -3 would produce the requried result (\(-5-3=-8\)), giving us, \(x^2-8x+15 + (x-5)(x-3)\).

The Quadratic Formula#

If all eelse fails, we can always rely on the quadratic formula. If we have a quadratic of the form \(ax^2 + bx + c = 0\), then the quadratic formula for the roots is:

\[ x = \frac{-b \pm\sqrt{b^2-4ac}}{2a} \]

Let’s write a Python function for the quadratic formula.

def quadratic_formula(a, b, c):
    """
    Returns the two solutions to the quadratic equation ax^2 + bx + c = 0. 
    
    :param a: Coefficient of x^2
    :param b: Coefficient of x
    :param c: Constant term
    :return: A tuple containing the two roots
    """
    discriminant = b**2 - 4 * a * c
    root1 = (-b + np.sqrt(discriminant)) / (2 * a)
    root2 = (-b - np.sqrt(discriminant)) / (2 * a)
    
    return root1, root2

We will use this function later on.

Example

Use the quadratic formula to solve the quadratic equation \(3x^2 - 5x + 2\).

Solution: As we are using the formula all we need to do is put in the values for \(a\), \(b\), and \(c\). So \(a=3\), \(b=-5\), and \(c=2\). Putting these into the equation yields:

\[\begin{split} \begin{aligned} x & = \frac{-b \pm\sqrt{b^2-4ac}}{2a} = \frac{-(-5) \pm\sqrt{(-5)^2-4(3\times 2)}}{2\times 3} \\ x & = \frac{5\pm\sqrt{25-24}}{6} = \frac{5\pm\sqrt{1}}{6} \end{aligned} \end{split}\]

Corresponding to the positive square root:

\[ x = \frac{5+1}{6} = 1 \]

And corresponding to the negative square root:

\[ x = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3} \]

So \(x=1\) and \(x=\frac{2}{3}\) are the roots.

We can now test out our function.

quadratic_formula(3, -5, 2)

(1.0, 0.6666666666666666)

solve(3 * x ** 2 - 5 * x + 2, x)

[2/3, 1]

The function agrees with the maths above and the sympy result.

Acid Dissociation

Formic acid is a weak acid with a dissociation constant \(K_a\) of \(1.8\times 10^{-4}\). the \(K_a\) relates the concentration of the H+ ions, denoted [H+ ions] and the amount of acid dissolved denotive \(N\), by the equation:

\[ K_a = \frac{[\textrm{H}^+]^2}{N - [\textrm{H}^+]} \]

Given that there are 0.1 moles of formic acid dissolved, calculate the pH of the solution.

Solution: To find the pH, first we need to find the concentration of H+ ions. Lets start by rearranging the equation for \(K_a\).

  • Multiply both sides by \((N-[\textrm{H}^+])\): \(K_a(N - [\textrm{H}^+]) = [\textrm{H}^+]^2\)

  • Expand the bracket: \(K_aN - K_a[\textrm{H}^+] = [\textrm{H}^+]^2\)

  • Take everything over to one side: \(0 = [\textrm{H}^+]^2 + K_a[\textrm{H}^+] - K_aN\)

The equation \([\textrm{H}^+]^2 + K_a[\textrm{H}^+] - K_aN = 0\) is a quadratic as \(K_a\) and \(N\) are constants and our variable (usually denoted \(x\)) is \([\textrm{H}^+]\).

We will put the symbols \(K_a\) and \(N\) into the quadratic formula and then put the numbers in afterwards to avoid complicating things. So as \(a=1\), \(b=K_a\), and \(c=-K_aN\), we have:

\[\begin{split} \begin{aligned} [\textrm{H}^+] & = \frac{-b\pm\sqrt{b^2-4ac}}{2a} = \frac{-K_a \pm \sqrt{K_a^2 - 4(-K_aN)}}{2} \\ [\textrm{H}^+] & = \frac{-K_a \pm \sqrt{K_a^2 + 4K_aN}}{2} \end{aligned} \end{split}\]

Putting the numbers given into that equation gives \([\textrm{H}^+] = 4.15\ldots\times 10 ^{-3}\) for the positive square root and \([\textrm{H}^+] = -4.33\ldots\times 10 ^{-3}\) for the negative square root. We can immediately disraged the negative answer, because you can’t have a negative concentration of H+.

The final stage is to calculate the pH, using the pH formula:

\[ \textrm{pH} = -\log_{10}{[\textrm{H}^+]} = -\log_{10}(4.15\times 10^{-3}) = 2.38\ldots \]

So pH is 2.4 (to 2 s.f.).

We can use the function above and assign appropraite variables to compute this with Python.

K_a = 1.8e-4
N = 0.1

roots = np.array(quadratic_formula(1, K_a, -K_a * N))

pH = -np.log10(roots[roots >= 0])
pH

array([2.38157583])

Above, we use numpy Boolean array indexing to find the positive root.

Contents