Complex Numbers

A complex number is a number that has both a real and imaginary component. They can be written in the form:

\[ a + bi \]

where \(a\) and \(b\) are real numbers and \(i=\sqrt{-1}\).

We often denote complex numbers by the letter \(z\), so \(z = a+bi\):

• \(a\) is the real part of \(z\), which we denote \(\textrm{Re}(z) = a\).

• \(b\) is the imaginary part of \(z\), which we denote \(\textrm{Im}(z) = b\).

• \(z^* = a-bi\) is called the complex conjugate of \(z = a+bi\).

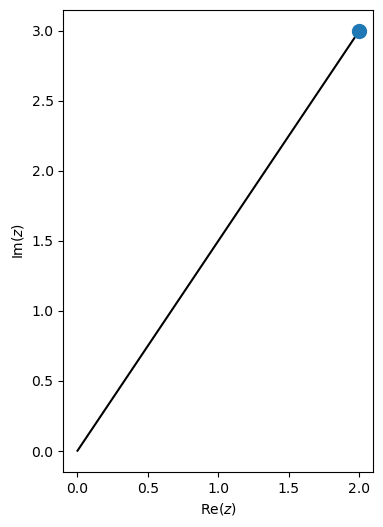
Just as we have a number line for real numbers, we can draw complex numbers on an x, y-axis called an Argand diagram with imaginary numbers of the y-axis and real numbers on the x-axis. We have drawn \(2+3i\) on the Argand diagram below.

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 2, 2)
y = 3 / 2 * x

fig, ax = plt.subplots(figsize=(4, 6))
ax.plot(x, y, 'k-')
ax.plot(x[-1], y[-1], 'o', ms=10)
ax.set_xlabel(r'$\text{Re}(z)$')
ax.set_ylabel(r'$\text{Im}(z)$')

plt.show()

Example

Find the imaginary and real parts of the following complex numbers, along with their complex conjugates:

1. \(z=-3+5i\)

2. \(z=1-2\sqrt{3}i\)

3. \(z=i\)

Solution:

1. For \(z=-3+5i\), we have \(\textrm{Re}(z) = -3\), \(\textrm{Im}(z) = 5\), and \(z^*=-3-5i\).

2. For \(z=1-2\sqrt{3}i\), we have \(\textrm{Re}(z) = 1\), \(\textrm{Im}(z) = -2\sqrt{3}\), and \(z^*=1+2\sqrt{3}\).

3. For \(z=i\), we have \(\textrm{Re}(z) = 0\), \(\textrm{Im}(z) = 1\), and \(z^*=-i\).

Different Form for Complex Numbers

When a complex number \(z\) is in the form \(z=a+bi\), we say it is written in Cartesian form. We can also write complex numbers in:

Note

These two forms are related via Euler’s formula, which has been referred to as “the most remarkable formula in mathematics”.

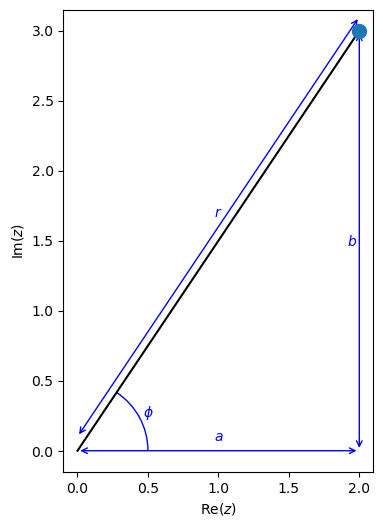
• Polar form: \(r(\cos{(\phi)} + i\sin{(\phi)})\)

• Exponential form: \(r\exp{(i\phi)}\)

where the magnitude \(|z|\) (or modulus) of \(z\) is the lenght \(r\)

\[ |z| = r = \sqrt{a^2 + b^2} \]

and the argument of \(z\) is the angle \(\phi\) (in radians)

\[ \arg{(z)}= \phi = \tan^{-1}\left(\frac{b}{a}\right) \]

This argument \(\phi\) is usually between \(-\pi\) and \(\pi\). Expressed mathematically, this is \(-\pi < \phi \leq \pi\).

We can see on the an Argand diagram, the relationship between the different forms for representing a complex number.

Show code cell source

Hide code cell source

from matplotlib.patches import Arc

fig, ax = plt.subplots(figsize=(4, 6))
ax.plot(x, y, 'k-')
ax.annotate("", xytext=(0, 0), xy=(2, 0), arrowprops=dict(arrowstyle="<->", color='b'))
ax.text(1, 0.1, '$a$', va='center', ha='center', color='b')
ax.annotate("", xytext=(2, 0), xy=(2, 3), arrowprops=dict(arrowstyle="<->", color='b'))
ax.text(2-0.05, 1.5, '$b$', va='center', ha='center', color='b')
ax.annotate("", xytext=(0, 0.1), xy=(2, 3.1), arrowprops=dict(arrowstyle="<->", color='b'))
ax.text(1, 1.7, '$r$', va='center', ha='center', color='b')
arc = Arc([0, 0], 1, 1, theta1=0, theta2=56.31, color='b')
ax.add_patch(arc)
ax.text(0.5, 0.27, '$\phi$', va='center', ha='center', color='b')

ax.plot(x[-1], y[-1], 'o', ms=10, zorder=10)

ax.set_xlabel(r'$\text{Re}(z)$')
ax.set_ylabel(r'$\text{Im}(z)$')

plt.show()

Example

Find the modulus and argument of the following complex numbers:

1. \(3+3i\)

2. \(-4+3i\)

3. \(-3i\)

4. 4

Solution:

1. For \(3+3i\), we have \(|z|=\sqrt{3^2 + 3^2} = \sqrt{18}\) and \(\arg{(z)}=\tan^{-1}\left(\frac{3}{3}\right) = \frac{\pi}{4}\;\textrm{rad}\).

2. For \(-4+3i\), we have \(|z|=\sqrt{(-4)^2 + 3^2} = 5\) and \(\arg{(z)}=\tan^{-1}\left(\frac{3}{-4}\right) = -0.64\;\textrm{rad}\).

3. For \(-3i\), we have \(|z|=\sqrt{0^2 + (-3)^2} = 3\) and \(\arg{(z)}=\tan^{-1}\left(\frac{-3}{0}\right)\).

   This calculation does not make sense, since we can’t divide by zero. However, if we imagine the Argand diagram, the argument is \(\arg{(z)}=\frac{\pi}{2}\;\textrm{rad}\), is the vector would be pointing negative along the \(\textrm{Im}(z)\) axis.

4. For \(4\), we have \(|z|=\sqrt{4^2 + 0^2} = 4\) and \(\arg{(z)}=\tan^{-1}\left(\frac{0}{4}\right) = 0\;\textrm{rad}\)

---

Python can natively handle complex numbers, but the numpy module is necessary to find the argument of a complex number, with the np.angle function.

z = complex(3, 3)
abs(z), np.angle(z)

(4.242640687119285, 0.7853981633974483)

The abs function is used to magnitude or modulus.

z = complex(-4, 3)
abs(z), np.angle(z)

(5.0, 2.498091544796509)

The numpy function is capable of handling the divide by zero appropriately.

z = complex(0, -3)
abs(z), np.angle(z)

(3.0, -1.5707963267948966)

z = complex(4, 0)
abs(z), np.angle(z)

(4.0, 0.0)

---

Example

Express \(4-5i\) in polar and exponential form.

Solution: First, we need to find the modulus and argument .

\[ |z| = r = \sqrt{4^2 + (-5)^2} = \sqrt{41}$ \]

and

\[ \arg{(z)} = \phi = \tan^{-1}\left(\frac{-5}{4}\right) = -0.9\;\textrm{rad} \]

So, in polar form, we have

\[ \sqrt{41}\left(\cos{(-0.9)} + i\sin{(-0.9)}\right) \]

and in exponential form,

\[ \sqrt{41}\exp{(-0.9i)} \]

Radial Wave Function

Written in the exponential form, the radial wave function for a 2p orbital of hydrogen is:

\[ \psi_{2\textrm{p}} = \mp \frac{1}{\sqrt{2}}r \sin{(\theta)}\exp{(\pm i\phi)} f(r) \]

Write this in polar form.

Solution: A complex number in exponential form: \(r\exp{(i\phi)}\) has the polar form \(r\left(\cos{(\phi)} + i\sin{(\phi)}\right)\).

Because of the \(\mp\) and \(\pm\) signs in this question, we have either:

\[ r = \frac{1}{\sqrt{2}}r\sin{(\theta)}f(r)\;\;\;\textrm{and}\;\;\;\phi = -\phi \]

OR

\[ r = -\frac{1}{\sqrt{2}}r\sin{(\theta)}f(r)\;\;\;\textrm{and}\;\;\;\phi = \phi \]

Hence in the polar form, we have either:

\[ r = \frac{1}{\sqrt{2}}r\sin{(\theta)}f(r)\left(\cos{(-\phi)} + i\sin{(-\phi)}\right) \]

OR r = -\frac{1}{\sqrt{2}}r\sin{(\theta)}f(r)\left(\cos{(\phi)} + i\sin{(\phi)}\right) $$

Applications

When using the quadratic formula:

\[ \frac{-b\pm\sqrt{b^2-4ac}}{2a} \]

we would not have known what to do if \(b^2-4ac\) was negative, however, now we are able to solve this square root using imaginary numbers.

Note

The two roots in this result at the complex conjugates of each other.

Example

Solve the equation \(x^2+3x+12\), using the quadratic formula.

Solution: So we have that \(a=1\), \(b=3\), and \(c=12\), so the quadratic formula gives:

\[\begin{split} \begin{aligned} \frac{-b\pm\sqrt{b^2-4ac}}{2a} & = \frac{-3\pm\sqrt{3^2-4\times 1\times 12}}{2\times 1} \\ & = \frac{-3\pm\sqrt{-39}}{2} \\ & = \frac{-3\pm i\sqrt{39}}{2} \end{aligned} \end{split}\]

This gives us \(x = \frac{-3 + i\sqrt{39}}{2}\) and \(x = \frac{-3 - i\sqrt{39}}{2}\).

---

As we would expect, sympy can help us with this.

Python Note

sympy, confusingly, uses the uppercase I to indicate \(i\).

from sympy import symbols, solve

x = symbols('x')

solve(x**2 + 3*x + 12, x)

[-3/2 - sqrt(39)*I/2, -3/2 + sqrt(39)*I/2]

But we can also use the quadratic formula, however, it is necessary that our inputs for \(a\), \(b\), and \(c\) are complex-type variables.

def quadratic_formula(a, b, c):
    """
    Returns the two solutions to the quadratic equation ax^2 + bx + c = 0. 
    
    :param a: Coefficient of x^2
    :param b: Coefficient of x
    :param c: Constant term
    :return: A tuple containing the two roots
    """
    discriminant = b**2 - 4 * a * c
    root1 = (-b + np.sqrt(discriminant)) / (2 * a)
    root2 = (-b - np.sqrt(discriminant)) / (2 * a)
    
    return root1, root2

quadratic_formula(1+0j, 3+0j, 12+0j)

((-1.5+3.122498999199199j), (-1.5-3.122498999199199j))

---